Test: Linear Algebra - 11 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Linear Algebra - 11
If 3x + 2y + z = 0, x + 4y+z = 0, 2x+ y + 4z = 0 be a system of equations, then
Let A be a square matrix and AT be its transpose matrix. Then A – AT is ….
Let T : C3 —> C3 be defined by T
 Then, the adjoint T* of T is given by
Then, the adjoint T* of T is given by 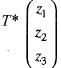 is equal to
is equal to

 Then, the adjoint T* of T is given by
Then, the adjoint T* of T is given by 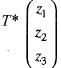 is equal to
is equal toHow many of the following matrices have an eigen value 1?
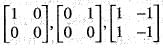 and
and 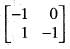
Let T : P3 ---> P3 be the map given by T(p(x))  . If the matrix of T relative to the standard basis B1, = B2 = {1, x, x2, x3} is M and M denotes the transpose of the matrix M, then M+ M is
. If the matrix of T relative to the standard basis B1, = B2 = {1, x, x2, x3} is M and M denotes the transpose of the matrix M, then M+ M is
Let T : Cn --> Cn be a linear operator having n distinct eigen values. Then,
Let T be a linear transformation from R3 —> R2 defined by T(x, y, z) = (x + y, y - z). Then, the matrix of T with respect to the ordered basis {(1, 1, 1), (1, -1, 0), (0, 1, 0)} and { ( 1 , 1 ),( 1 ,0 )} is
Let V = {p(x) : p(x) ≠ 0 and p(x) of degree 2} be a set of all non-zero polynomial in x of degree 2 is not a vector space, because of
If A = 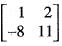 has the eigen values 3 and 9, then the eigen values of A3 are
has the eigen values 3 and 9, then the eigen values of A3 are
Let T be a linear transformation given by the matrix (occurring in a typical transportation problem)
 then
then
One of the eigen values of matrix 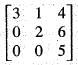 is 5, then the corresponding eigen vector is
is 5, then the corresponding eigen vector is
Consider the vector space R3 and the maps f g : R3 —> R3 defined by f ( x , y, z) = (x, | y |, z) and g(x, y, z) = (x + 1, y - 1, z). Then,
The number of different n x n symmetric matrices with each element being either 0 or 1, is
Consider the following statements:
S1: The sum of two singular n x n matrices may be non-singular.
S2. The sum of two n x n non-singular matrices may be singular.
Q. Which of the following statements is true?
Let the linear transformation S and T : 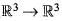 be defined by
be defined by
S(x, y, z) = (2x, 4x-y, 2x + 3y-z)
and T(x, y, z) = (x cos θ - y sin θ, x sin θ + y cos θ, z)
where 0 < θ < π/2. then,
Let Ax = b be a system of linear equations where A is an m x n matrix and b is an m x 1 column vector and X is an n x 1 column vector of unknown. Which of the following is false?
Let the linear transformation T : F2--> F3 be defined by T(x1, x2) = (x1, x1 + x2, x2). Then, the nullity of T is
|
27 docs|150 tests
|




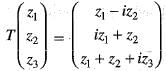
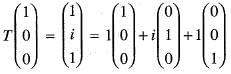
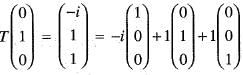
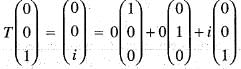
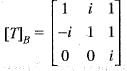
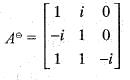
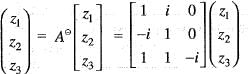
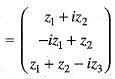
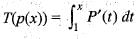
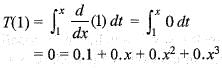
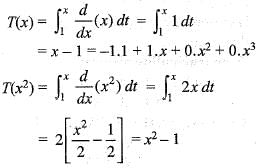
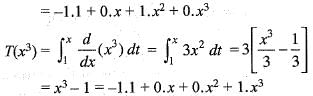
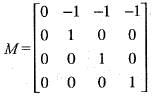

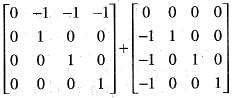

 is
is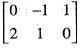
 are
are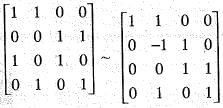
 Therefore, Rank T = 3. Also det (T) = 0. Hence, T is unimodular.
Therefore, Rank T = 3. Also det (T) = 0. Hence, T is unimodular.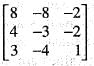 is
is 











