Test: Linear Algebra - 2 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Linear Algebra - 2
A set of linear equations is given in the form Ax = b, where A is a 2 × 4 matrix with real number entries and b ≠ 0. Will it be possible to solve for x and obtain a unique solution by multiplying both left and right sides of the equation by AT (the super script T denotes the transpose) and inverting the matrix AT A?
Consdierthe subspace W = {(x1, x2,.... ,x10) 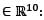 xn = xn-1 + xn - 2 for 3 < n < 10) of the vector space
xn = xn-1 + xn - 2 for 3 < n < 10) of the vector space 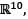 the dimension of W is
the dimension of W is
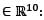 xn = xn-1 + xn - 2 for 3 < n < 10) of the vector space
xn = xn-1 + xn - 2 for 3 < n < 10) of the vector space 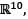 the dimension of W is
the dimension of W isWhich one of the following is a subspace of the vector space 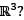
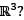
If A and B are 3 × 3 real matrices such that rank (AB) = 1, then rank (BA) cannot be
Which of the following sets of functions from 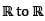 is a vector space over
is a vector space over 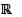
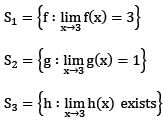
Let T : R3 → R3 be the linear transformation define by T(x, y, z) = (x + y, y+ z, z + x) for all (x, y, z) ∈ 3. Then
Let V be a 3 dimensional vector space over the field 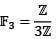 of 3 elements. The number of distinct 1 dimensional subspaces of V is
of 3 elements. The number of distinct 1 dimensional subspaces of V is
Let M = {(a1,a2,a3): ai ∈ (1,2,3,4); a1 + a2 + a3 = 6} then the number of elements in M is
The dimension of the vector space of all symmetric matrices A = (aij) of order n x n (n > 2) with real entries, aii = 0 and trace zero is
Let n be a positive integer and let Hn be the space of all n x n matrices A = (aij) with entries in 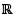 satisfying aij = ars whenever i + j = r + s (i, j, r, s = 1, 2,..., n) then the dimention of Hn, as a vector space over
satisfying aij = ars whenever i + j = r + s (i, j, r, s = 1, 2,..., n) then the dimention of Hn, as a vector space over 
The dimension of the vector space of all symmetric matrices of order n x n (n > 2) with real entries and trace equal to zero is
Let {X,Y,Z) be a basis of R3 Consider the following statements P and Q
P : {X + Y,Y + Z, X - Z) is a basis of R3
Q : {X + Y + Z,X + 2Y - Z, X - 3Z} is a basis of R3
Which of the above statements hold true?
Suppose A is a real n × n matrix of rank r. Let V be the vector space of all real n × n matrices X such that AX = 0. What is the dimension of V?
Consider the subspace W = {[aij] : aij = 0, if i is even) of all 10 x 10 matrices(real) then the dimension of W is
If V1 and V2 are 3-dimensional subspaces of a 4-dimensional vector space V, then the smallest possible dimension of V1 ∩ V2 is _______.
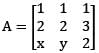 and let V = {(x, y, z)
and let V = {(x, y, z) 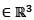 : |A| = 0}.Then the dimension of V equals
: |A| = 0}.Then the dimension of V equals
A basis of V = {(x, y, z, w) ∈ R4: x + y - z = 0, y + z + w = 0, 2x + y - 3z = 0)
|
27 docs|150 tests
|





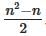 . Now, in your case the diagonal is not zero but the sum of its elements is zero, that means that you have n−1 elements which can vary. SO you get
. Now, in your case the diagonal is not zero but the sum of its elements is zero, that means that you have n−1 elements which can vary. SO you get 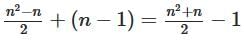 as expected.
as expected.

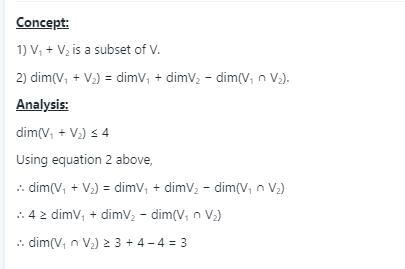
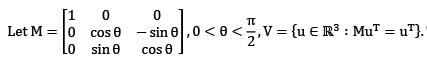 Then the dim V is
Then the dim V is











