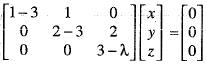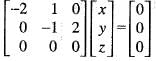Test: Linear Algebra - 6 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Linear Algebra - 6
Find the value of k for which the following simultaneous equations
x + y + z = 3; x + 2y + 3z = 4; x + 4y + kz = 6 will not have a unique solution.
x + y + z = 3; x + 2y + 3z = 4; x + 4y + kz = 6 will not have a unique solution.
Solution for the system defined by the set of equations 4y + 3z = 8; 2x - z = 2 and 3x + 2y = 5 is
Consider the system of simultaneous equation
x + 2y + z = 6;
2x+y + 2z = 6;
x+y + z = 5
This system has
x + 2y + z = 6;
2x+y + 2z = 6;
x+y + z = 5
This system has
Consider the system x + y + z = 0; x - y - z = 0, then the system of equations have
If the linear transformation T : R2 → R3 is such that T(1, 0) = (2,3,1) and T(1,1) = (3, 0,2), then
The unique linear transformation T : R2 → R2 such that T(1,2) = (2,3) and T(0, 1) = (1,4). Then, the rule for T is.
For a linear transformation T : R10 → R6, the kernal has dimension 5. Then, the dimension of the range of T is
Let P2[x] be the vector space of all polynomials over R of degree less than or equal to 2. Let D be the differential operator on P2[x]. Then, matrix of D relative td the basis [x2, 1, x] is equal to
If T : V2(R) → V3(R) defined as T(a, b) = (a + b , a-b ,b) is a linear transformation, Then nullity of T is
The transition matrix P from the standard ordered basis to the ordered basis {(1, 1), (-1,0)} is
Let F be any field and let T be a linear operator on F2 defined by T(a, b) = (a + b, a), then T-1(a, b) is equal to:
A linear transformation T : R2 → R2 such that T(3, 1) = (2, -4) and T(1, 1) = (0,2). Then, T(7, 8) is
A is any matrix which satisfy A3 - A2 + A - I = 0 and A3x3, then A4 is
Which one of the following is an eigen vector of the matrix 
The eigen vectors o f the matrix  are written in the form
are written in the form  and
and 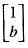 . What is a + b ?
. What is a + b ?
|
27 docs|150 tests
|



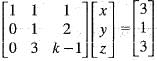
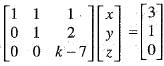
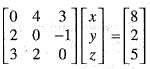
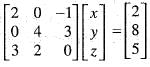

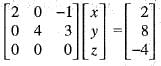



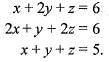



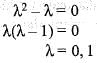
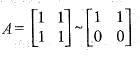

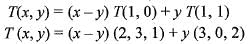
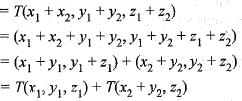
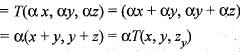 Hence, T is a linear.
Hence, T is a linear.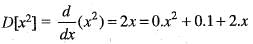
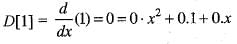
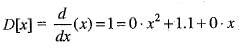 Therefore, the matrix of D related to the basis {x2, 1, x} is
Therefore, the matrix of D related to the basis {x2, 1, x} is 
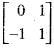
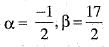
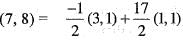
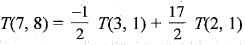
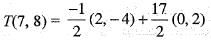
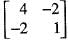 are
are
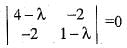


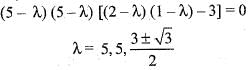
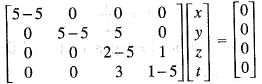
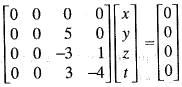
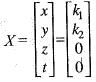
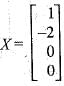
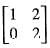 are
are  and
and 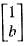 . We need to find the value o f a + b. The characteristic equation o f the given matrix is, |A - λI| = 0
. We need to find the value o f a + b. The characteristic equation o f the given matrix is, |A - λI| = 0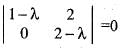
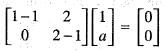
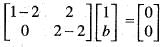
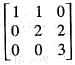 is
is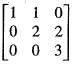
 = 0
= 0