Test: Linear Algebra - 7 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Linear Algebra - 7
Let T be a linear operator on a finite dimensional space V and c is any scalar, then c is characteristic value of T if
Let T be a linear transformation on the vector space V2(F) defined by T (a, b) = (a, 0), the matrix of T relative to the ordered basis {(1, 0), (0,1)} of V2(F) is
Let V be a vector space and T is a linear operator on V. If W is a subspace of V, then W is invariant under T iff α ∈ T implies
A linear transformation E on V isa projection on some subspace iff
Let T : V -> V be a non-singular linear transformation, then
Let T : V --> U be a linear transformation such that T maps independent sets into independent sets, then
For the matrix A = 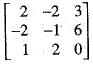 one of the eigen values is 3.
one of the eigen values is 3.
The other two eigen values are
Consider the following matrix A = 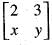 . If the eigen values of A are 4 and 8, then
. If the eigen values of A are 4 and 8, then
The characteristic equations of a (3 x 3) matrix A is defined as a(λ) = | λ | - Al = λ3 + λ2 + 2λ + 1 = 0. If l denotes identity matrix, then the inverse of matrix A will be
Let T : R3 —> R2 be a linear transformation defined by T(x, y, z) = (x + y, x - z). Then the dimension of the null space of T is
For n ≠ m , let T1 : Rn —> Rm and T2 : Rm —> Rn be linear transformations such that T1T2 is bijective. Then
Let T: R3 ---> R3 be the linear transformation whose matrix with respect to the standard basis of R3 is 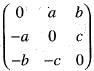 where a, b, c are real numbers not all zero. Then T
where a, b, c are real numbers not all zero. Then T
Let T : R2---> R2 be a linear transformation such that T(1,2) = (2, 3) and T(0, 1) = (1, 4). Then T(5, 6) is
Let S = T : R3 —> R3 ; T is a linear transformation with T(1,0,1) = (1, 2, 3), T(1,2, 3) = (1,0,1)}. Then S is
Let V be the vector space of all 6 × 6 real matrices over the field . Then the dimension of the subspace of V consisting of all symmetric matrices is
Let T : R3 ---> R3 be a linear transformation and I be the identity transformation of R3. If there is a scalar c and a non-zero vector x ∈ R3 such that T(x) = cx, then rank (T - cl)
For a positive integer n, let Pn denote the space of all polynomials P(x) with coefficients in R such that degree P(x) ≤ n and let Bn denote the standard basis of Pn given by Bn= 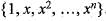
If T : P3 ---> P4 is the linear transformation defined by 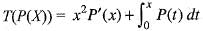 and A = (aij) is the 5 x 4 matrix of T with respect to the standard bases B3 and B4 then
and A = (aij) is the 5 x 4 matrix of T with respect to the standard bases B3 and B4 then
|
27 docs|150 tests
|


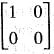

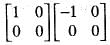 and
and 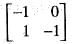
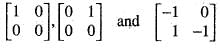
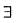 only one matrix which has eigen value 1.
only one matrix which has eigen value 1. has an
has an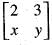 has the eigen values 4 and 8. We need to find the values of x and y.
has the eigen values 4 and 8. We need to find the values of x and y.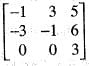 are
are
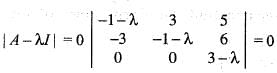
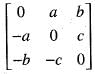 where a, b, c are real number not all zero. The determinant
where a, b, c are real number not all zero. The determinant 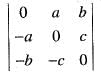 = -abc + bac = 0
= -abc + bac = 0

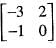 , then calculate A9.
, then calculate A9.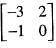
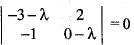
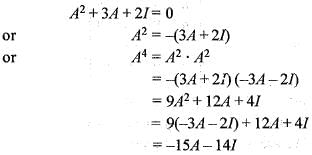
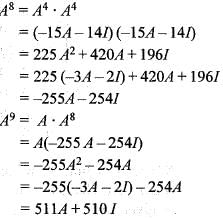
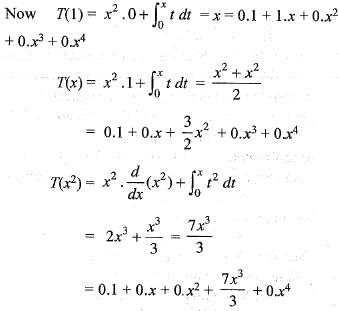
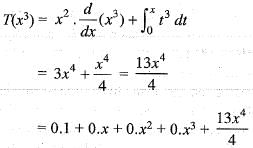
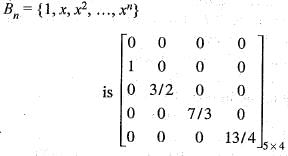 Hence a32 = 3/2 and a33 = 0
Hence a32 = 3/2 and a33 = 0










