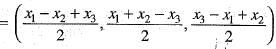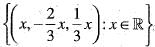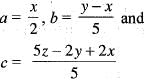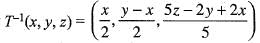Test: Linear Algebra - 8 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Linear Algebra - 8
Consider the linear transformation T : R7----> R7 defined by T (x1, x2,......, x6, x7) = (x7, x6,..........,x2,x1)
Q. Which of the following statements is true.
Q. Which of the following statements is true.
Let x, y be linearly independent vectors in R2. Suppose T : R2 ----> R2 be a linear transformation such that T(y) = αx and T(x) = 0 then with respect to some basis in R2, T is of the form
The characteristic polynomial of 3 x 3 matrix A |λI - A| = λ3 + 3λ2 + 4λ - 3
Let x - trace (A) and y = |A|, the determinant of A.
Then,
Let x - trace (A) and y = |A|, the determinant of A.
Then,
The characteristic vector of the matrix 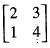 corresponding to characteristic root 1 is
corresponding to characteristic root 1 is
A system o f linear equations x + 2 y - z = l l , 3 x + y - 2 z = 10, x - 3y = 5 has
The number of onto linear transformation from R3 to R4 is
Suppose T1 : V —> U and T2 : U ---> W be a linear transformations then
Let V be the vector space of polynomial functions of degree three or less. Let the ordered basis for V consisting of the functions of the four functions xj : j = 0, 1, 2, 3 and let D be the differentiation operator. Then the matrix of D in the above ordered basis is
Let T : R2 ---> R2 be a linear transformation defined by
T(x, y) = (x - y , 2x + y)
Then T-1 is
Let A = 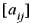 be an n x n matrix such that aij = 3,
be an n x n matrix such that aij = 3, and j. Then the nullity of A is
and j. Then the nullity of A is
The system of simultaneous linear equations
x + y + z = 0
x - y - z = 0 has
Minimal polynomial m(x) of Anxn each of whose element is 1, is
Let T : R3 --> R3 be defined by T(x1, x2, x3) = (x1 + x2, x2 + x3, x3 + x1) Then T-1 is
Let T be a linear operator on R3 defined by
T(1, 0,0) = (1,2,1)
T(0, 1,0) = (3, 1,5)
T(0,0,1) = (3,-4, 7)
Then
Let F be a field and T be a linear operator on F2 defined by T(x1, x2) = (x1 + x2, x1). Then T-1(x1, x2) is
Let T :R3---> R3: be a linear transformation defined by T(x, y, z) = (2x, 2x - 5y, 2y + z). Then T-1 is
|
27 docs|150 tests
|


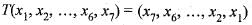
 be an ordered basis of R
be an ordered basis of R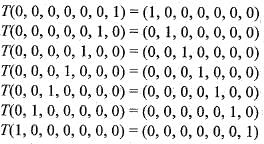 So, the matrix corresponding to linear transformation T with respect to basis B is
So, the matrix corresponding to linear transformation T with respect to basis B is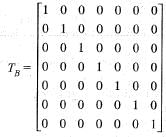
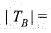
 = 1
= 1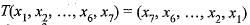
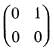

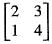 corresponding to the characteristic root 1.
corresponding to the characteristic root 1.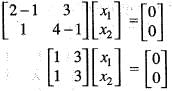
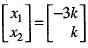 or
or 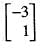
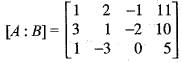


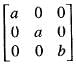 is
is
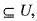 we also have T2(T1(V))
we also have T2(T1(V)) 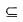 T2(U) and
T2(U) and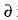 is
is
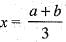 and
and 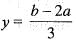
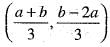
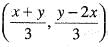
 , then the eigen values of A are
, then the eigen values of A are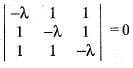
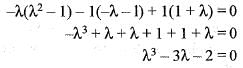
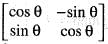 be such that A has real eigen values, then
be such that A has real eigen values, then has real eigen values. The characteristic equation of the given matrix is,
has real eigen values. The characteristic equation of the given matrix is, and j.
and j.

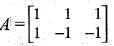


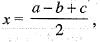
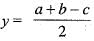
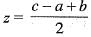

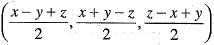 Hence,T-1(x1, x2, x3)
Hence,T-1(x1, x2, x3)