Test: Linear Algebra - 9 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Linear Algebra - 9
Let T be the linear operator on R3 defined by T(x1, x2, x3) = ( 2x1, x1 - x2, 5x1 + 4x2 + x3). Then T-1 is
The eigen values of a 3 x 3 real matrix A are 1,2 and - 3. Then
Let A be 3 x 3 matrix whose characteristic roots are 3 ,2 ,-1 .
If B = A2 - A, then |B| is
Let T : Cn —> Cn be a linear operator of rank n - 2. Then,
Choose the correct matching from A, B, C and D for the transformation T1, T2 and T3 (mappings from R2 to R3) as defined in Group 1 with the statements given in Group 2
Group 1
P.T1x( x, y) = (x , x, 0)
Q.T2(x,y) = (x, x +y ,y)
R.T3(x,y) = (x,x+1,y)
Group 2
1. Linear transformation of rank 2
2. Not a linear transformation
3. Linear transformation of rank 1
Let V, W and X be three finite dimensional vector spaces such that dim V = dim X, Suppose S : V --> W and T : W ---> X are two linear maps such ToS : V --> X is injective.Then,
Let S and T be two linear operators on R3 defined by
S (x,y,z) = (x,x + y , x - y - z )
T(x , y , z) = (x + 2z ,y - z ,x + y + z)
Let A be the matrix of quadratic form (x1- x2 + 2x3)2.
Then, trace of A is
The eigen values of a 3 x 3 real matrix P are 1, -2, 3. Then,
The system of equations
x + y + z = 0
3x + 6y + z = 0
αx + 2y + z = 0
has infinitely many solutions, then a is equal to
Consider the system of linear equation
x + y + z = 3, x - y - z = 4, x - 5 y + kz = 6
Then, the value of k for which this system has an infinite number of solution is
Real matrices [A]3x1,[B]3x3, [C]3 x 5 [D]5 x 3, [E]5 x 5 and [F]5 x 1, are given. Matrices [B] and [E] are symmetric. Following statements are made with respect to these matrices:
(i) Matrix product [F]T [C]T [B] [C] [F] is a scalar.
(ii) Matrix product [D]T [F] [D] is always symmetric. With reference to above statements, which of the following applies?
Match List I with List II and select the correct answer using the codes given below in the lists.

Codes

Let T:R2→R2 be a linear transformation such that T(1,-1) = (1,0), T(2,-1)=(0,1). Then T(-3,2) equals to
|
27 docs|150 tests
|


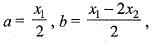
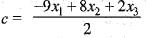
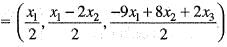


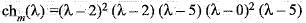 Hence, the minimal polynomial of the given matrix M is,
Hence, the minimal polynomial of the given matrix M is,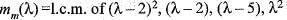
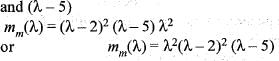

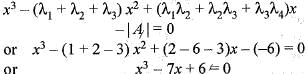
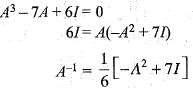
 is
is 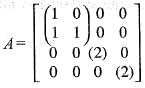
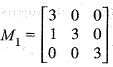
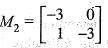
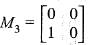
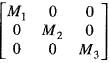 is
is
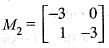
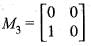
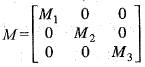
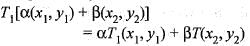
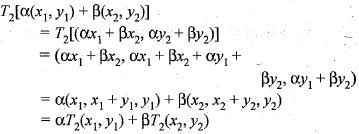 Hence, T2 is a linear transformation.
Hence, T2 is a linear transformation.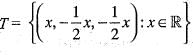
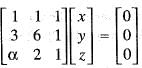
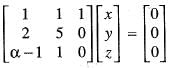
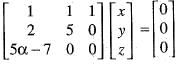
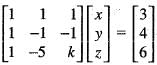
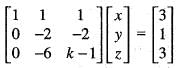
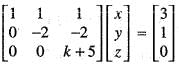
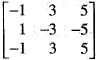 is
is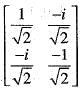 is
is











