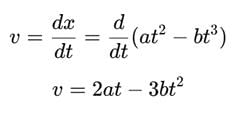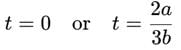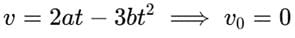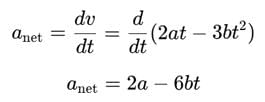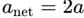Test: Motion in a Straight Line (May 23) - NEET MCQ
15 Questions MCQ Test - Test: Motion in a Straight Line (May 23)
The displacement x of a particle depend on time t as x = at2 - bt3
A particle has intial velocity 10 m/s. It moves due to constant retarding force along the line of velocity which produces a retardation of 5 m/s2. Then -
A particle initially at rest is subjected to two forces. One is constant, the other is a retarding force proportion at to the particle velocity. In the subsequent motion of the particle
Let v and a denote the velocity and acceleration respectively of a body
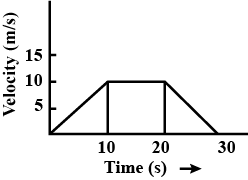
The figure shows the velocity (v) of a particle plotted against time (t)
A particle moves with constant speed v along a regular hexagon ABCDEF in the same order. Then the magnitude of the average velocity for its motion from A to -
A projectile of mass 1 kg is projected with a velocity of m/s such that it strikes on the same level as the point of projection at a distance of
m. Which of the following options are incorrect.
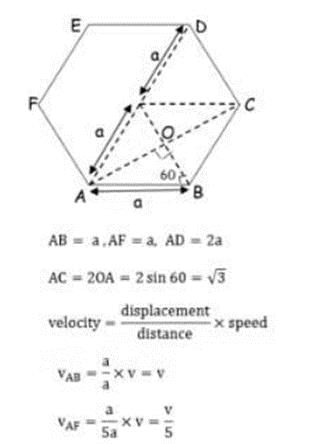
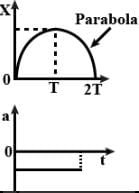
The x-t graph of the particle moving along a straight line is shown in figure.
The a-t graph of the particle is correctly shown by
The figure shows a velocity-time graph of a particle moving along a straight line
Choose the incorrect statement. The particle comes to rest at
A train covers 60 miles between 2 p.m. and 4 p.m. How fast was it going at 3 p.m.?
The figure shows a velocity-time graph of a particle moving along a straight line
The maximum of displacement of the particle is
In the following graph, distance travelled by the body in metres is
A car, initially at rest travels 20 m in 4 sec along a straight line with constant acceleration. Find the acceleration of car?
An aircraft has a take-off velocity of 50 m/s. What length of runway is needed if the aircraft's average acceleration along the ground is 2.5 m/s2?