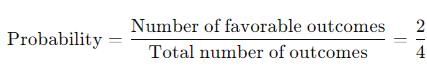Test: Probability And Expected Value By Mathematical Expectation- 4 - CA Foundation MCQ
30 Questions MCQ Test Quantitative Aptitude for CA Foundation - Test: Probability And Expected Value By Mathematical Expectation- 4
If probability of drawing a spade from a well-shuffled pack of playing cards is ¼ then the probability that of the card drawn from a well-shuffled pack of playing cards is ‘not a spade’ is
Probability of the sample space is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Sum of all probabilities is equal to
Let a sample space be S = {X1, X2, X3} which of the fallowing defines probability space on S ?
Let P be a probability function on S = {X1 , X2 , X3} if P(X1)= ¼ and P(X3) = 1/3 then P (X2) is equal to
The chance of getting a sum of 10 in a single throw with two dice is
The chance of getting a sum of 6 in a single throw with two dice is
P (B/A) defines the probability that event B occurs on the assumption that A has happened
The complete group of all possible outcomes of a random experiment given an ________ set of events.
When the event is ‘certain’ the probability of it is
The classical definition of probability is based on the feasibility at subdividing the possible outcomes of the experiments into
Two unbiased coins are tossed. The probability of obtaining ‘both heads’ is
Two unbiased coins are tossed. The probability of obtaining one head and one tail is
Two unbiased coins are tossed. The probability of obtaining both tail is
Two unbiased coins are tossed. The probability of obtaining at least one head is
When 3 unbiased coins are tossed. The probability of obtaining 3 heads is
When unbiased coins are tossed. The probability of getting both heads or both tails is
Two dice with face marked 1, 2, 3, 4, 5, 6 are thrown simultaneously and the points on the dice are multiplied together. The probability that product is 12 is
A bag contain 6 white and 5 black balls. One ball is drawn. The probability that it is white is
Probability of occurrence of at least one of the events A and B is denoted by
Probability of occurrence of A as well as B is denoted by
Which of the following relation is true ?
If events A and B are mutually exclusive, the probability that either A or B occurs is given by
The probability of occurrence of at least one of the 2 events A and B (which may not be mutually exclusive) is given by
If events A and B are independent, the probability of occurrence of A as well as B is given by
For the condition P(AB)= P(A)P(B) two events A and B are said to be
The conditional probability of an event B on the assumption that another event A has actually occurred is given by
In a throw of coin what is the probability of getting tails.
Demand of products per day for three days are 21, 19, 22 units and their respective probabilities are 0.29, 0.40, 0.35. profit per unit is $0.50 then expected profits for three days are
If P (A)= 1/2, P(B)= 1/2, the events A & B are
|
148 videos|174 docs|99 tests
|
|
148 videos|174 docs|99 tests
|
Top Courses for CA Foundation
Important Questions for Probability And Expected Value By Mathematical Expectation- 4
Probability And Expected Value By Mathematical Expectation- 4 MCQs with Answers
Online Tests for Probability And Expected Value By Mathematical Expectation- 4 Quantitative Aptitude for CA Foundation
|
© EduRev
|
Education Revolution
|
Follow Us
|
