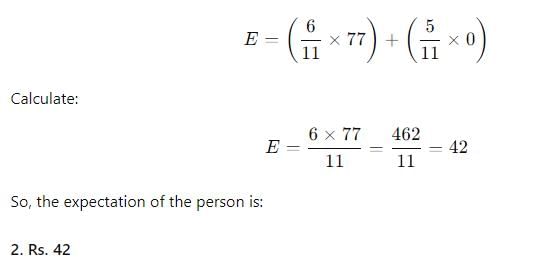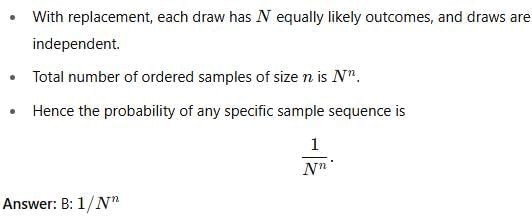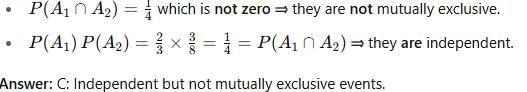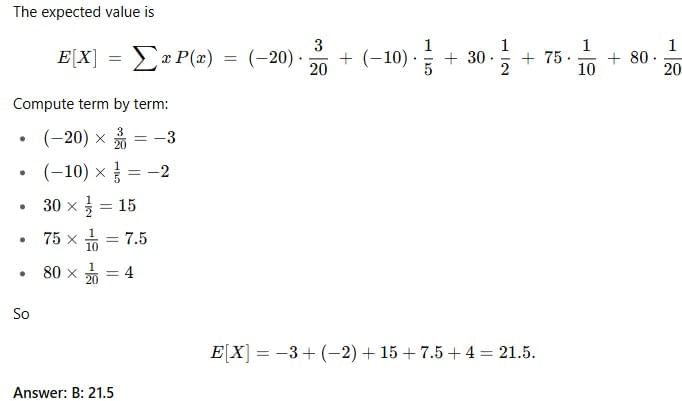≈ 0.7143
Test: Probability And Expected Value By Mathematical Expectation- 6 - CA Foundation MCQ
30 Questions MCQ Test Quantitative Aptitude for CA Foundation - Test: Probability And Expected Value By Mathematical Expectation- 6
The probability of winning of a person is 6/11 and at a result he gets Rs.77/= .The expectation of this person is
A family has 2 children. The probability that both of them are boys if it is known that one of them is a boy
The Probability of the occurrence of a no. greater then 2 in a throw of a die if it is known that only even nos. can occur is
A player has 7 cards in hand of which 5 are red and of these five 2 are kings. A card is drawn at random. The probability that it is a king, it being known that it is red is
In a class 40 % students read Mathematics, 25 % Biology and 15 % both Mathematics and Biology. One student is select at random. The probability that he reads Mathematics if it is known that he reads Biology is
In a class 40 % students read Mathematics, 25 % Biology and 15 % both Mathematics and Biology. One student is select at random.The probability that he reads Biology if he reads Mathematics
Probability of throwing an odd no with an ordinary six faced die is
For a certain event A ,P (A) is equal to
When none of the outcomes is favourable to the event then the event is said to be
The probability of selecting sample of size 'n' out of a population of size N by simple random sampling with replacement is:
If P(A) = 0.45, P(B) = 0.35 and P(A & B) = 0.25, then P(A/B)=?
Find the probability of drawing a spade on each of two consecutive draws from a well shuffled pack of cards, without replacement
If a pair of dice is thrown then the probability that the sum of the digit is neither 7 nor 11 is _____.
A player tosses 3 fair coins. He wins Rs.5 if three appear, Rs.3 if two heads appear, Rs.1 if one head occurs. On the other hand, he losses Rs.15 if 3 tails occur. Find expected gain of the player.
The probability of a cricket team winning match at Kanpur is 2/5 and losing match at Delhi is 1/7. what is the Probability of the term winning at least one match?
Two coins are tossed simultaneously. Find the probability of getting exactly one head.
For any two events A1, A2 letP(A1) = 2/3,P(A2) = 3/8 and P(A1 ∩ A2) =1/4 then A1, A2 are:
Find the expected value of the following probability distribution

The odds against A solving a certain problem are 4 to 3 and the odds in favour of B solving the same problem are 7 to 5. What is the probability that the problem will be solved if they both try?
A box contains 2 red, 3 green and 2 blue balls. Two bails are drawn at random. What is the probability that none of the balls drawn is blue?
A bag contains 2 red, 3 green and 2 blue balls. Two balls are drawn at random. What is the probability that none of the balls drawn is blue?
An urn contains 2 red and 1 green balls. nother urn contains 2 red and 2 green balls. An urn was selected at random and then a ball was drawn from it. If it was found to be red then the probability that it has been drawn from urn one is ______.
Find the expected value of the following probability distribution
A bag contains 6 red balls and some blue balls. If the probability of drawing a blue ball form the bag is twice that of a red ball, find the number of blue balls in the bag
A company employed 7 CA's, 6 MBA's and 3 Engineer's. In how many ways the company can form a committe, if the committee has two members of each type.
In a packet of 500 pens, 50 are found to be defective. A pen is selected at random. Find the probability that it is non defective.
A bag contains 5 Red balls, 4 Blue Balls and 'm' Green Balls. If the random probability of picking two green balls is 1/7. What is the no. of green Balls (m).
Four married couples have gathered in a room. Two persons are selected at random amongst them, find the probability that selected persons are a gentleman and a lady but not a Couple.
The odds against A solving a certain problem are 4 to 3 and the odds in favour of B solving the same problem are 7 to 5. What is the probability that the problem will be solved if they both try?
One Card is drawn from pack of 52, what is the probability that it is a king or a queen?
|
101 videos|276 docs|89 tests
|