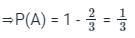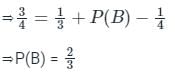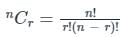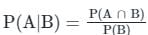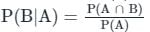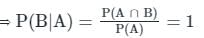Test: Probability (संभावना) - Bank Exams MCQ
10 Questions MCQ Test - Test: Probability (संभावना)
52 ताश के पत्तों के एक पैकेट में से एक पत्ता निकाला जाता है। इसकी क्या प्रायिकता है कि निकाला गया पत्ता पान या बादशाह का है?
यदि 2 पासे फेंके जाते हैं, तो दोनों पासों पर समान अंक आने की प्रायिकता क्या है?
यदि P(A ∪ B) = 3/4, P(A ∩ B) = 1/4, P(A̅) = 2/3, तो P(B) का मान ज्ञात कीजिए।
A और B दो घटनाएं इस प्रकार हैं जिससे P(B) = 0.4 और P(A ∪ B) = 0.6 हैं। यदि A और B स्वतंत्र हैं तो P(A) का मान क्या है?
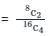
एक कमरे में आठ जोड़े हैं। उनमें से यदि 4 लोगों को यादृच्छिक पर चुना जाता है तो प्रायिकता क्या है कि वे जोड़े हो सकते हैं?
जब एक सिक्का 6 बार उछाला जाता है तो संभावित परिणामों की संख्या क्या है?
चार पासे को उछाला जाता है। तो उन संभव परिणामों की संख्या क्या है जिसमें कम से कम एक पासा 2 दर्शाता है?
यदि A और B दो घटनाएं इस प्रकार हैं जिससे P(A) ≠ 0 और P(B | A) = 1 है, तो निम्न में से कौन-सा सही है?
यदि एक सिक्के को तीन बार उछाला जाता है तो सिक्के में एक या दो शीर्ष आने की प्रायिकता ज्ञात करें।
मान लीजिए P(A) = 0.4, P(B) = P और P(A ∪ B) = 0.7। यदि A और B स्वतंत्र घटनाएँ हैं तो P का मान क्या है?