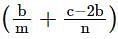Test: Quadratic Equations- 2 - CAT MCQ
10 Questions MCQ Test Quantitative Aptitude (Quant) - Test: Quadratic Equations- 2
Find the value of a/b + b/a, if a and b are the roots of the quadratic equation x2 + 8x + 4 = 0?
Find the quadratic equations whose roots are the reciprocals of the roots of 2x2 + 5x + 3 = 0?
A man could buy a certain number of notebooks for Rs.300. If each notebook cost is Rs.5 more, he could have bought 10 notebooks less for the same amount. Find the price of each notebook?
I. a2 - 7a + 12 = 0,
II. b2 - 3b + 2 = 0 to solve both the equations to find the values of a and b?
Let f(x) be a quadratic ploynomial in x such that f(x) ≥ 0 for all real numbers x. If f(2) = 0 and f(4) = 6, then f(-2) is equal to
Let r and c be real numbers. If r and -r are roots of 5x3 + cx2 - 10x + 9 = 0, then c equals
Suppose k is any integer such that the equation 2x2 + kx + 5 = 0 has no real roots and the equation x2 + (k - 5)x + 1 = 0 has two distinct real roots for x. Then, the number of possible values of k is
If (3 + 2√2) is a root of the equation ax2 + bx + c = 0, and (4 + 2√3) is a root of the equation ay2 + my + n = 0, where a, b, c, m and n are integers, then the value of 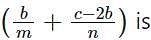
If r is a constant such that |x2 – 4x - 13| = r has exactly three distinct real roots, then the value of r is?
|
191 videos|133 docs|110 tests
|