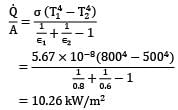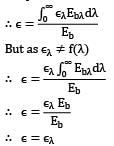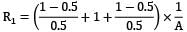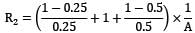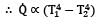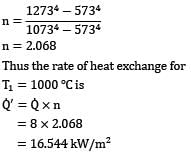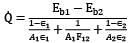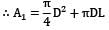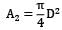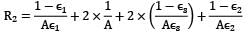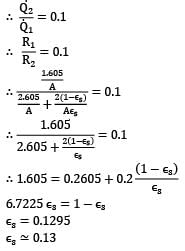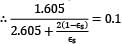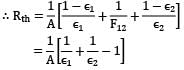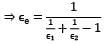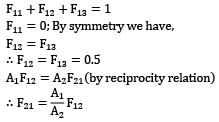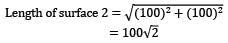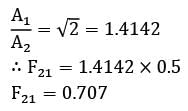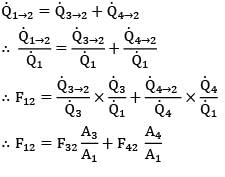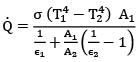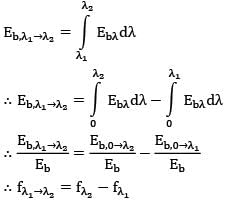Test: Radiative Heat Transfer Level - 2 - Chemical Engineering MCQ
20 Questions MCQ Test - Test: Radiative Heat Transfer Level - 2
What is net radiation heat exchange per square meter per unit time for two very large plates at temperature values of 800 K and 500 K? Emissivities of hot and cold plates are 0.8 and 0.6 respectively. Stefan-Boltzmann constant is - 5.67x10-8W/m2K4
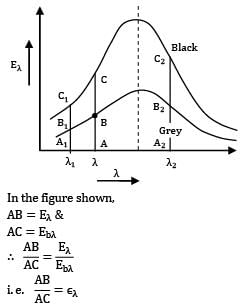
The spectral hemispherical absorptivity of an opaque surface is as shown.
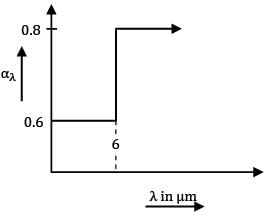
The surface is exposed to ir-radiation for which the spectral distribution is as shown.
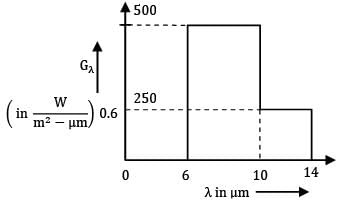
What is the total hemispherical absorptivity of surface?


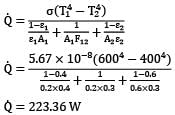
Two grey surfaces that form an enclosure exchange heat with one another by thermal radiation. Surface 1 has a temperature of 400 K, an area of and a total emissivity of 0.4. Surface 2 has a temperature of 600 K, area of and a total emissivity of 0.6. If the view factor is 0.3, the rate of radiation heat transfer between the two surfaces is
Which of the following statements is false regarding spectral distribution of thermal radiation emitted by a grey surface P. Monochromatic emissivity is independent of wavelength Q. Total emissivity is equal to monochromatic emissivity.
R. (monochromatic emissive power) Vs λ( graph for the surface at a
given temperature is scaled down version of the graph for black body at same temperature.
S. The wavelength corresponding to maximum monochromatic emissive power is same as that of grey surface at same temperature.
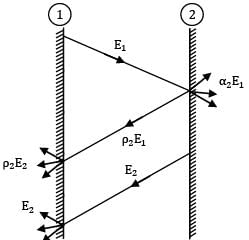
Two infinitely large parallel plates 1 & 2, facing each other are separated by a very small gap. The plates are exchanging heat by thermal radiation and gap between them is filled with non-participating medium. Surface 1 is a black surface with temperature equal to and surface 2 is a grey surface with temperature equal to and emissivity equal to 0.8. Find out the radiosity for surface 2 in kW/m2
Two large parallel grey plates with a small gap between them, exchange radiation at the rate of when their emissivities are 0.5 each. By coating one plate, its emissivity is reduced to 0.25. Temperatures remain unchanged. The new rate of heat exchange shall become
An enclosure consists of four surfaces 1, 2, 3 and 4. The view factors for radiation heat transfer (where the subscripts 1, 2, 3, 4 refer to the respective surfaces) are F11 = 04 and F13 = 0.25. The surface areas A1 and A4 are 4m2 respectively. The view factor is
The net radiation heat exchange rate between a heating element at a temperature of 800oC and inner wall of a furnace maintained at . The heat exchange rate when the element temperature is increased to 1000oC for the same furnace temperature is
A filament of 75 W light bulb may be considered as a black body radiating into a black enclosure at . The filament diameter is 0.1 mm and length is 5 cm. Considering only radiation, the filament temperature is
Consider a surface at 0oC that may be assumed to be a blackbody in an environment at . If of radiation is incident on the surface, the radiosity of this black surface is
A solar flux of intensity directly strikes a space vehicle surface which has an absorptivity of 0.4 and emissivity of 0.6. The equilibrium temperature of this surface in space at 0 K is
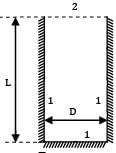
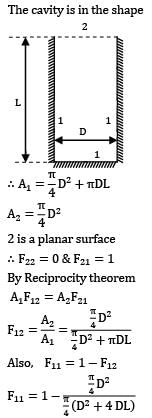
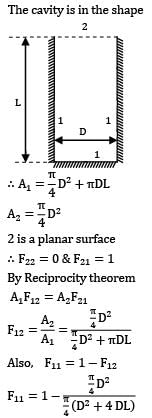
The shape factor of a cylindrical cavity (open from top) with respect to itself is __________. L & D are length and diameter of the cavity respectively.
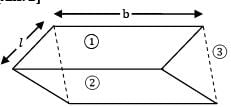
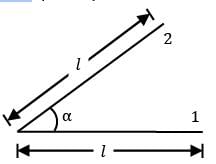
What is the view factor for inclined parallel plates of equal width and a common edge? The width of plates to the plane of paper is b. (b >>L)
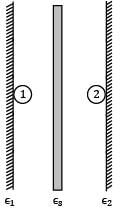
Two very large parallel plates separated by vacuum are maintained at uniform temperatures T1= 750K & T2=500K and have emissivities ε1= 0.85 and ε2 = 0.7 respectively. If a thin aluminium sheet with same emissivity on both sides is placed in between the plates, the rate of heat transfer between the plates reduces by 90%. The emissivity of aluminium sheet is given as
For the radiation between two infinite parallel planes of emissivity respectively, which one of the following is the expression for emissivity factor or equivalent emissivity?
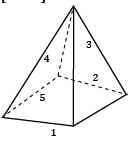
Determine the view factors from the base of the pyramid shown in figure to each of its four side surfaces. The base of the pyramid is a square and its side surfaces are isosceles triangles.
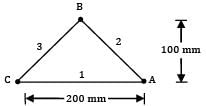
Determine for the following configuration. Long inclined plates (point B is directly above the center of )

Consider surfaces ① & ② as shown in the figure.
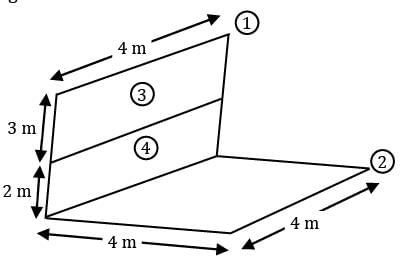
Surface ① is divided into two parts ③ & ④. Which of the following options is correct expression for F12
What is the equivalent emissivity for radiant heat exchange between a small body ( in a very large enclosure (emissivity = 0.5)?
Determine the percentage of radiation emitted by the sun within the visible spectrum ( Wavelengths from 0.4 μm (violet) to 0.76 μm(red), considering the sun to be black body and its effective surface temperature to be 5800 K. Given black body radiation function for 2320μmk is 0.124509 and for 4408μmk is 0.550015 .