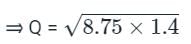Test: Ratio and Proportion (अनुपात और समानुपात) - Bank Exams MCQ
15 Questions MCQ Test - Test: Ratio and Proportion (अनुपात और समानुपात)
8.75 और 1.4 का मध्यानुपाती क्या है?
जब 11, 16, 26 और 36 प्रत्येक में a जोड़ा जाता है, तो इस क्रम में प्राप्त संख्याएँ समानुपात में होती हैं। a और a + 5 का मध्यानुपाती क्या है?
रहीम की मासिक आय 12,000 रुपये है तथा अमित की वार्षिक आय 191520 रुपये है। यदि प्रत्येक का मासिक व्यय 9960 रुपये है, तो उनकी बचतों में अनुपात ज्ञात कीजिए ।
एक व्यक्ति के पास 25 पैसे, 50 पैसे और 1 रुपये के सिक्के हैं। कुल 220 सिक्के हैं और कुल राशि 160 है। यदि जितने 25 पैसे के सिक्के हैं उसका तीन गुना 1 रुपये के सिक्के हैं, तो 50 पैसे के सिक्कों की संख्या क्या है?
एक 35 ग्राम वजन के हीरे, जिसका मूल्य 12,250 रुपये है, को दो टुकड़ों में काट दिया जाता है, जिनका वजन 5 ∶ 2 के अनुपात में है। यदि मूल्य, वजन के वर्ग के समानुपाती है, तो हानि ज्ञात कीजिए।
750 रुपये को A, B और C के बीच इस तरह से विभाजित किया गया है कि A : B, 5 : 2 और B : C, 7 : 13 है। A का हिस्सा क्या है?
A और B के मासिक वेतन 5 : 6 के अनुपात में है। यदि उन दोनों के वेतन में 2000 रुपये की वृद्धि की जाती है, तब नया अनुपात 11 : 13 हो जाता है। A का नया मासिक वेतन कितना है?
राहुल के पास एक थैले में 1 रुपए, 50 पैसे और 25 पैसे के सिक्के हैं और सिक्कों की संख्या का अनुपात 1 ∶ 1/2 ∶ 1/3 है। यदि राहुल के पास कुल 1120 रुपए हैं, तब 25 पैसे के सिक्कों का कुल मूल्य ज्ञात कीजिए।
एक बैग में ₹ 2, ₹ 5 और ₹ 10 के सिक्कों के मूल्यवर्ग में ₹ 785 है। सिक्के 6 : 9 : 10 के अनुपात में हैं। बैग में ₹ 5 के कितने सिक्के हैं?
एक परिवार में, पिता, माता, पुत्र और पौत्र की आयु क्रमशः A, B, C और D है। यदि A - B = 3, B + C = 78, C + D = 33 और परिवार की औसत आयु 34 वर्ष है, तो (B - C) का मान ज्ञात कीजिए।
एक थैले में 5 पैसे, 10 पैसे और 25 पैसे के सिक्के 3 : 2 : 1 के अनुपात में हैं। यदि कुल मिलाकर इसमें 60 रुपये हैं, तो उसमें 5 पैसे के कितने सिक्के हैं?
यदि a : b = 3 : 2 है, b : c = 2 : 1 है, c : d = 1/3 : 1/7 है और d : e = 1/4 : 1/5 है, तो a : b : c : d : e ज्ञात कीजिये।
u : v = 4 : 7 और v : w = 9 : 7। यदि u = 72, तो w का मान क्या है?
N और G मिलकर एक दिन में जितना कमाते हैं, उतना S, 5 दिनों में कमाता है। S और N मिलकर एक दिन में जितना कमाते हैं, उतना ही G अकेले 3 दिनों में कमाता है। क्रमशः N, G और S की दैनिक आय का अनुपात ज्ञात कीजिए।
यदि दो संख्याओं a और b का लघुत्तम समापवर्त्य 108 है और उनका महत्तम समापवर्तक 36 है तो उनका माध्य अनुपात ज्ञात कीजिए।