Test: Real Analysis- 1 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Real Analysis- 1
If A = {a, b, c} and R = {(a, a), (a, b) ( b, c), (b, b), (c, c), (c, a)} is a binary relation on A, then which one of the following is correct?
If the cardinality of a set A is 4 and that of a set B is 3, then what is the cardinality of the set A Δ B?
Assertion (A): If events, A, B, C and D are mutually exhaustive, then (A ∪ B ∪ C)c = D.
Reason (R): (A ∪ B ∪ C)c = D implies if any element is excluded from the sets A, B and C, then it is included in D.
Reason (R): (A ∪ B ∪ C)c = D implies if any element is excluded from the sets A, B and C, then it is included in D.
Elements of a population are classified according to the presence or absence of each of 3 attributes A, B and C. What is the number of smallest ultimate classes into which the population is divided?
If A and B are subsets of a set X, then what is {A ∩( X - B)} } ∪ B equal to?
The total number of subsets of a finite set A has 56 more elements, then the total number of subsets of another finite set B. What is the number of elements in the set A?
Consider the following statement.
I. Parallelism of lines is an equivalence relation.
II. xRy, if x is a father of y, is an equivalence relation. Which of the statements given above is/are correct?
If A and B are disjoint sets, then A ∩ (A' ∪ B) is equal to which one of the following?
Let U= { 1 , 2 , 3 , ...,20}. Let A, B, C be the subsets of U.
Let A be the set of all numbers, which are prefect squares, B be the set of all numbers which are multiples of 5 and C be the set of all numbers, which are divisible by 2 and 3.
Q. Consider the following statements.
I. A, B, C are mutually exclusive.
II. A, B, C are mutually exhaustive.
III. The number of elements in the complement set of A∪ B is 12.
Q. Which of the statements given above the correct?
If A = P {1, 2} where P denotes the power set, then which one of the following is correct?
Let R and S be two equivalence relations on a set A.
Then,
If (1 + 3 + 5 + ...+ p )+ (1 + 3 + 5 + ...+ q) = ( l + 3 + 5 + ... + r) where each set of parentheses contains the sum of consecutive odd integers as shown, what is the smallest possible value o f (p + q + r) where p > 6?
Let A = {x | x ≤ 9 , x ε N}. Let B = {a, b, c} be the subset of A where (a + b + c) is a multiple of 3. What is the largest possible number of subsets like B?
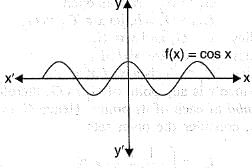
A mapping f: R → R which is defined a s f( x ) = cos x; x ε R is
If n(A) = 115, n{B) = 326, n(A — B) = 47, then what is n(A ∪ B) equal to?
In a town of 10000 families it was found that 40% family buy newspaper A, 20% buy newspaper B and 10% families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2% families buy all the three newspaper, then number of families which buy A only is
A survey shows that 63% of the Americans like cheese whereas 76% like apples. If x% of the Americans like both cheese and apples, then
|
27 docs|150 tests
|


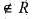

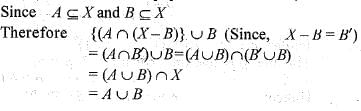
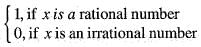

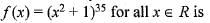
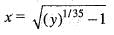 Thus, every real number has no pre-image.
Thus, every real number has no pre-image.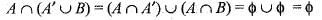
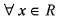 is one- one but not onto. Since, range ≠ codomain, so f(x) is into.
is one- one but not onto. Since, range ≠ codomain, so f(x) is into.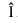 A implies (a, a )
A implies (a, a ) 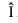 R and (a, a)
R and (a, a)  S,
S,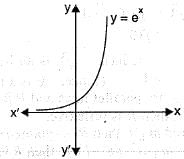
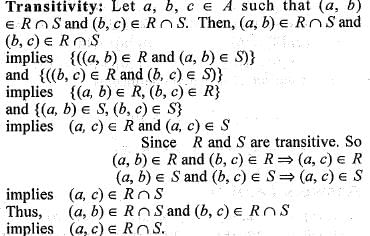

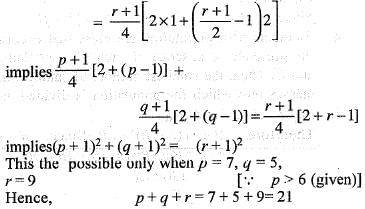
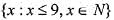
 Codomain of f(x) = R
Codomain of f(x) = R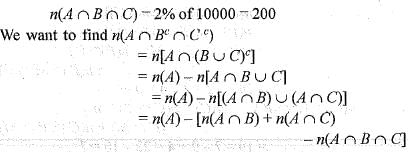 = 4000 - [500 + 400 - 200]
= 4000 - [500 + 400 - 200]