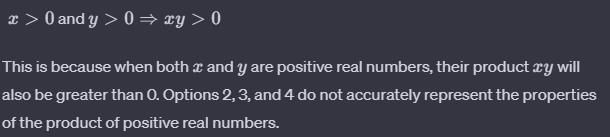
Test: Real Analysis- 4 - Mathematics MCQ

Nowhere dense is a strengthening of the condition "not dense" (every nowhere dense set is not dense, but the converse is false). Another definition of nowhere dense that might be helpful in gaining an intuition is that a set S⊂X is nowhere dense set in X if and only if it is not dense in any non-empty open subset of X (with the subset topology).

For example, Z is nowhere dense in RR because it is its own closure, and it does not contain any open intervals (i.e. there is no (a,b) s.t. (a,b)⊂Z¯=Z An example of a set which is not dense, but which fails to be nowhere dense would be {x∈Q|0<x<1}. Its closure is [0,1], which contains the open interval (0,1). Using the alternate definition, you can note that the set is dense in (0,1)⊂R.

An example of a set which is not closed but is still nowhere dense is {1n|n∈N}. It has one limit point which is not in the set (namely 00), but its closure is still nowhere dense because no open intervals fit within {1n|n∈N}∪{0}.

If  {a_n} is convergent, Then {b_n} and {c_n} both are convergent. 
because {b_n} and {c_n} are sub sequence of {a_n}

The number of elements in power set of A is 1.
[Since, P(A) = 2° = 1]
So, P{P(A} = 2¹ = 2
or P{P{P{(A)}} - 2² - 4
or P{P{P{P(A)}}} = 2⁴ = 16

Here, R = { ( x , y ) : | x² - y² | < 16}
and given A = {1,2, 3,4, 5}
So, R = {(1,2),(1,3)(1,4); (2,1)(2,2) (2,3)( 2 ,4); (3,1)(3 ,2 )(3 ,3) (3,4); (4,1), (4,2)(4,3); (4,4)(4,5) (5,4) (5,5)}

Suppose that F is an ordered field and S is a nonempty subset of F. An upper bound for S is any element M of F so that x ≤ M for all x ∈ S. A least upper bound for S is any element L of F which is an upper bound for S and which also has the property that every a < L is not an upper bound for S: L is the smallest upper bound for S. 5 For example, if S is the set of integers which are less than π, then S is nonempty because 1 ∈ S, and S has an upper bound because π > x for all x ∈ S. S also has a least upper bound, namely 3. If T is the set of numbers T = { −1,− 1/2 ,− 1/3 ,− 1/4 ,− 1/5 ,...} , then T is visibly nonempty, and also T has an upper bound: any positive number is an upper bound, since all of the elements of T are negative. The least upper bound for T is 0. The set Z of all integers has no upper bound and has no least upper bound.

Informally, the theorems state that if a sequence is increasing and bounded above by a supremum, then the sequence will converge to the supremum; in the same way, if a sequence is decreasing and is bounded below by an infimum, it will converge to the infimum.

We have R⁻¹ = {(5,4), ( 4, 1), (6, 4), (6, 7), (7, 3)}
We now obtain the elements of R⁻¹o R. We first pick the element of R and then R⁻¹
Since (4, 5) ∈ R and (5, 4) ∈R⁻¹ We have (4, 4) ∈ R⁻¹o R
Similarlly
(1,4)∈R,(4,1)∈R−1⇒(1,1)∈R⁻¹oR.
(4,6)∈R,(6,4)∈R−1⇒(4,4)∈R⁻¹oR.
(4,6)∈R,(6,7)∈R−1⇒(4,7)∈R⁻¹oR.
(7,6)∈R,(6,4)∈R−1⇒(7,4)∈R⁻¹oR.
(7,6)∈R,(6,7)∈R−1⇒(7,7)∈R⁻¹oR.
(3,7)∈R,(7,3)∈R−1⇒(3,3)∈R⁻¹oR.
Hence
R⁻¹o R = { (1, 1), (4, 4), (4, 7), (7, 4), (7, 7), (3, 3)}

Since A is not a subset of B, complement of B contains A. Hence A and complement of B are not disjoint.