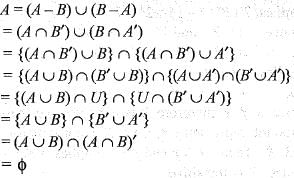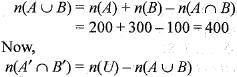Test: Real Analysis - 5 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Real Analysis - 5
If S is a set of real numbers, and c1 and c2 are two least upper bounds of S, then
Let R = {(1,3 ), (2,2), (3 ,2 )} and S = {(2 ,1 ) (3,2), (2 ,3 )} be two relations of set ,4 = {1 , 2 ,3 } . Then , RoS is equal to
Statement (A): Set S of real number is bounded above, if sup S is finite.
Statement (B): Set S of real numbers is unbounded above, if sup S = ∞
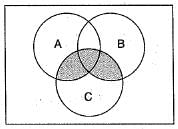
What does the shaded region in the following diagram represent?
An integer m is said to be related to another integer n, if m is a multiple of n. Then, the relation is
The order of a set A is 3 and that of a set B is 2. What is the number of relations from A to B?
Which one of the following is correct?
Here, P(A) denotes the power set of a set A.
Let A = {x : x ∈ R, | x | < 1};
B = { x : x ∈ R, |x — 1| ≥ 1} and A ∪ B = R - D , then the set D is
“Every non-empty set S of real numbers which is bounded above has supremum” is
For real numbers x and y, we write xRy <=> x - y + √2 is an irrational number. Then, the relation R is
If A and B are two sets satisfying A - B = B - A, then which one of the following is correct?
Sets A and B have n elements in common. How many elements will (A x B) and (B x A) have in common?
If (A - B) ∪ (B - A) = A for subsets A and B of the universal set U, then which one of the following is correct?
The equation of the curve for which the square of the ordinate is twice the rectangle contained by the abscissa and the intercept of the normal on x-axis and passing through (2, 1) is
Let A = {(x, y) : y = ex, x ∈ R}, B = {(x, y) : y = e-x,x ∈ R}. Then
If A, B and C are three sets and U is the universal set such that n(U) = 700, n(A) = 200, n(B) = 300 and h (A ∩ B) = 100, then what is the value of (A' ∩ B')?
|
27 docs|150 tests
|



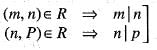
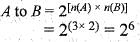
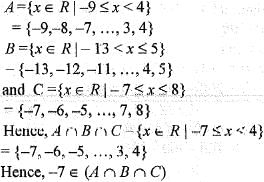
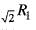 and
and 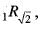 R is not transitive also because
R is not transitive also because 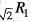 and
and 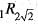 but
but 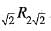 .
.