Test: Real Analysis - 6 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Real Analysis - 6
Let A and B be two sets such that n(A) = 0.16, n(B) = 0.14, n(A ∪ B) = 0.25. Then n(A ∩ B) is equal to
20 teachers of a school either teach Mathematics of Physics. 12 of them teach Mathematics while 4 teach both the subjects. Then, the number of teachers teaching Physics only is
If U is the universal set and P is a subset of U, then what is P ∩ {(P - U ) ∪ ( U - P ) } equal to?
Two Unite sets have m and n elements. The total number of subsets of the first set is 56 more than the total number of subsets of the second set. The values of m and n are
In the set A = {1,2,3,4, 5}, a relation R is defined by R = {(x , y ) | x, y ∈ A and x < y } . Then,R is
If A and B are two subsets of a set X, then what is A ∩ (A ∪ B)' equal to?
For non-empty subsets A, B and C of a set X such that A ∪ B = B ∩ C, which one of the following is the strongest inference that can be derived?
The relation R = {(1,1), (2,2), (3,3), (1,2), (2,3), (1,3)} on a set A = { 1 ,2 , 3} is
In a class of 100 students, 55 students have passed in Mathematics and 67 students have passed in Physics. Then, the number of student who have passed in Physics only, is
Let R1 be a relation defined by R1 = {(a, b ) | a ≥ b, a, b ∈ R}. Then R1 is
Of the members of three athletic teams in a school 21 are in the cricket team, 26 are in the hockey team and 29 are in the football team. Among them, 14 play hockey and cricket, 15 play hockey and football, and 12 play football and cricket. 8 play all the three games. The total number of members in the three athletic teams is
In a class of 30 pupils, 12 take needle work, 16 take Physics and 18 take History. If all the 30 students take atleast one subject and no one takes all three, then the number of pupils taking 2 subjects is
For a set A, consider the following statements
1. A ∪ P(A) = P(A)
2. {A} ∩ P(A)=A
3. P(A) - {A} = P{A}
where P denotes power set.
Which of the statements given above is/are correct?
The number of elements in the set
{(a, b) : 2a2 + 3b2 = 35, a b ∈ Z}, where Z is the set of all integer, is
If two sets A and B are having 99 elements in common, then the number of elements common to each of the sets A x B and B x A are
Assertion (A): y = 2x + 3 is a one-to-one real-valued function.
Reason (R): x1 ≠ x2 ==> y1 ≠ y2, y1 = 2 x1 + 3, y2 = 2x2 + 3, for any two real x1, and x2
If A, B and C are three finite sets, then what is [(A ∪ B) ∩ C]' equal to
Consider the following statements
1. φ ∈ {φ}
2. {φ} 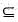 φ
φ
Which of the statements given above is/are correct?
|
27 docs|150 tests
|



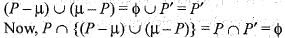
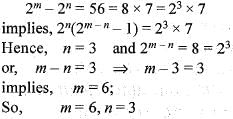
 x, therefore R is not reflexive. Also, x<y does not imply that
x, therefore R is not reflexive. Also, x<y does not imply that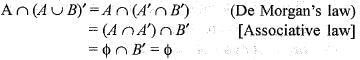
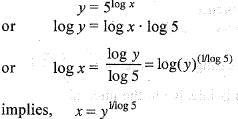
 B
B  C
C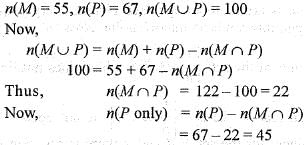
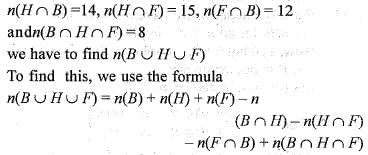
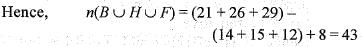 Thus, these are 43 members in all
Thus, these are 43 members in all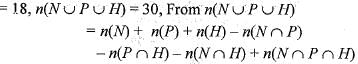
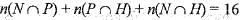
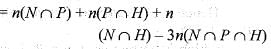 = 16 - 0 =16
= 16 - 0 =16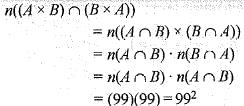
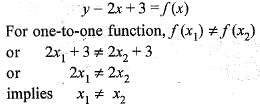
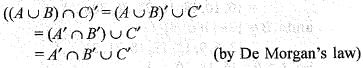
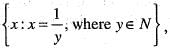 then
then