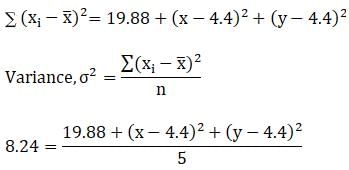Test: Statistics- 1 - JEE MCQ
25 Questions MCQ Test - Test: Statistics- 1
A batsman scores runs in 10 innings 38,70,48,34,42,55,63,46,54 and 44, then the mean deviation is
If the angle between two lines of regression is 900, then it represents
The two lines of regression are 2x - 7y + 6 = 0 and 7x – 2y +1 = 0. What is correlation coefficient between x and y ?
The two lines of regression are x + 4y = 3 and 3x +y = 15. value of x for y = 3 is
The mean of 5 observations is 4.4 and their variance is 8.24. If three observations are 1,2 and 6, the other two observations are
If x and y are related as y – 4x = 3, then the nature of correlation between x and y is
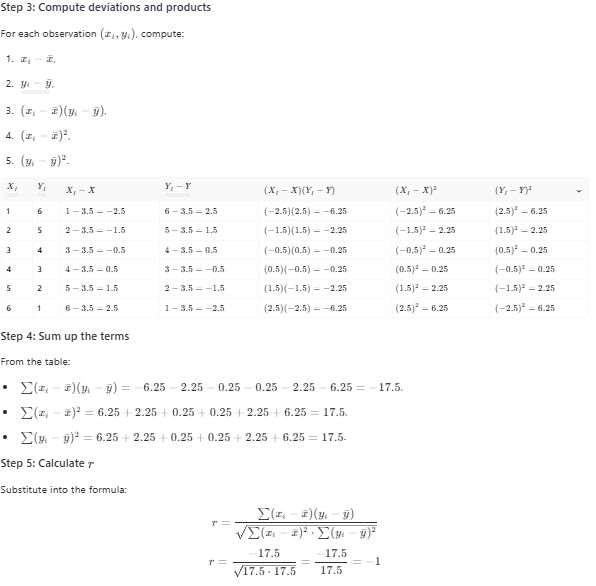
Coefficient of correlation between the observations (1, 6) , (2 , 5) , (3 , 4) , (4 , 3) , (5 , 2) , (6 , 1) is
If the two lines of regression of a bivariate distribution coincide, then the correlation coefficient ρ satisfies.
For a moderately skewed distribution, quartile deviation and the standard deviation are related by
Which one of the following average is most affected of extreme observations ?
The Mode of the following items is 0,1,6,7,2,3,7,6,6,2,6,0,5,6,0.
The statistical method which helps us to estimate or predict the unknown value of one variable from the known value of the related variable is called
S.D. of a data is 6. When each observation is increased by 1, then the S.D. of new data is
The mean weight of a group of 10 items is 28 and that of another group of n items is 35.The mean of combined group of 10 + n items is found to be 30. The value of n is
The measure of variation which is least affected by extreme items is
A group of 10 items has mean 6. If the mean of 4 of these items is 7.5, then the mean of the remaining items is
If the coefficient of variation between x and y is 0.28, covariance between x and y is 7.6, and the variance of x is 9, then the S.D. of the y series is
The Q.D. of the daily wages (in Rs) of 7 persons given below: 12,7,15,10,17,19,25 is
Which of the following is not a measure of central tendency :
If the mean of numbers 27,31,89,107,156 is 82, then the mean of 130,126,68,50,1 is :
If in moderately asymmetrical distribution mode and mean of the data are 6 μ and 9 μ respectively, then median is