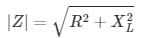Test: Step Response of First Order Circuits - 1 - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: Step Response of First Order Circuits - 1
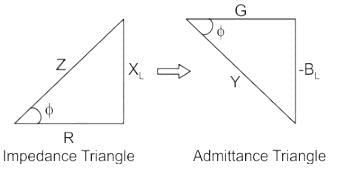
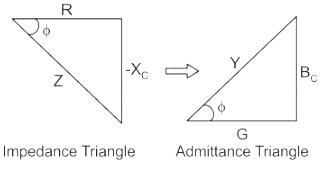
Calculate the power factor of a series RL circuit having the conductance of 30 Siemens and the susceptance of 40 Siemens.
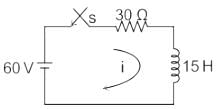
A series RL circuit (as shown in fig) has a constant voltage V = 60 V applied at t = 0. Determine the current flowing through the inductor.

Time constant in an R-L circuit is defined as the time taken by the current to become
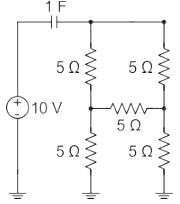
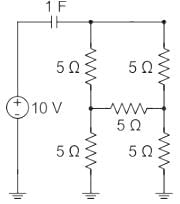
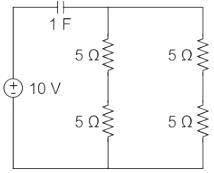
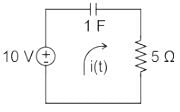
The initial charge in the 1 F capacitor present in the circuit shown is zero. The energy in joules transferred from the DC source until steady state condition is reached equals _________. (Give the answer up to one decimal place.)
A series RL circuit having a resistance of 20 Ω and inductance of 8 H is connected to a DC voltage source of 120 V at t = 0. The current in the circuit at t = 0.6 sec is
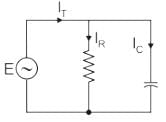
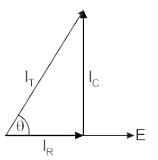
What is the phase angle between the capacitor current and the applied voltage in a parallel RC circuit?
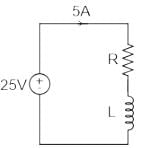
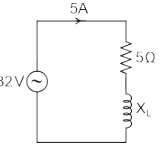
A coil takes a current of 5 A when connected to a 25 V DC supply. To obtain the same current with a 50 Hz AC supply, the voltage required was 32 V. Calculate the inductive reactance and power factor of the coil.
Inductive load of resistance 20 Ω and inductance 0.1 H is connected in series and switched on to an AC voltage of V = 100 sin(200 t + α). Find the angle α such that there is no transients?
An RL circuit has a resistance of 3 ohms and a reactance of 4 ohms, the impedance of the circuit is
A switch is connected in between a 12 V battery and an uncharged capacitor and a 1 KΩ resistor. At the time instant when the switch is closed, the voltage across the capacitor is:



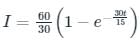

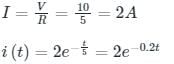
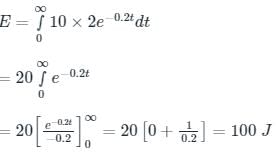

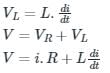
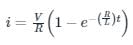
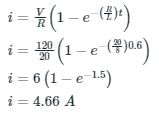

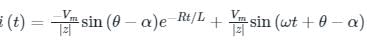
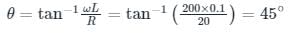 ⇒ α = 45°
⇒ α = 45°