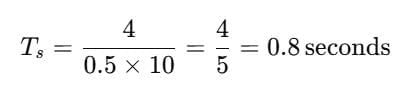Test: Step Response of Second Order Circuits - Electrical Engineering (EE) MCQ
15 Questions MCQ Test - Test: Step Response of Second Order Circuits
In the figure shown, the ideal switch has been open for a long time.
If it is closed at t = 0, then the magnitude of the current (in mA) through the 4kΩ resistor at t = 0+ is _______.

Which of the following is true for the step response of a second-order system when the damping ratio ζ is greater than 1?
Which of the following quantities give a measure of the transient characteristics of a control system, when subjected to unit step excitation.
1. Maximum overshoot
2. Maximum undershoot
3. Overall gain
4. Delay time
5. Rise time
6. Fall time
1. Maximum overshoot
2. Maximum undershoot
3. Overall gain
4. Delay time
5. Rise time
6. Fall time
The time response of a second-order system with damping ratio ζ=0.6\zeta = 0.6 ζ=0.6 is shown. The peak time tp is the time when the system reaches its first maximum. What is the peak time in seconds?
The output in response to a unit step input for a particular continuous control system is c(t)= 1-e-t. What is the delay time Td?
For a second-order system with a damping ratio of 0.2 and a natural frequency of 1 rad/s, the time to reach 90% of the final value is approximately:
The peak percentage overshoot of the closed loop system is :
What is the time required for a second-order system with damping ratio ζ = 0.5 and natural frequency ωn = 10 rad/s to reach 98% of its final value?
Given a second-order system with damping ratio ζ = 0.7 and natural frequency ωn = 15 rad/s, calculate the rise time for the unit step response.
The unit step response of a second order system is = 1-e-5t-5te-5t . Consider the following statements:
1. The under damped natural frequency is 5 rad/s.
2. The damping ratio is 1.
3. The impulse response is 25te-5t.
Which of the statements given above are correct?
The unit step response of a second-order system with a damping ratio of 0.2 and natural frequency of 5 rad/s is given by:
c(t) = 1 - e^(-0.2t) * (cos(4.9t) + (0.2/0.2) * sin(4.9t))
What is the maximum overshoot in this system?
For the system 2/s+1, the approximate time taken for a step response to reach 98% of its final value is:
For a critically damped second-order system, what is the time constant τ?
Consider a system with transfer function G(s) = s + 6/Ks2 + s + 6. Its damping ratio will be 0.5 when the values of k is:
A second-order system with damping ratio ζ = 0.5 has a natural frequency of 10 rad/s. What is the overshoot for the step response of this system?


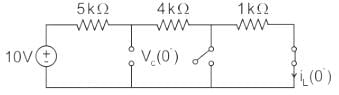
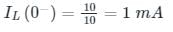
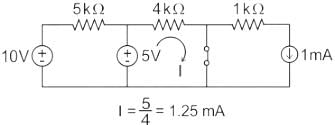 I = 5/4 = 1.25mA
I = 5/4 = 1.25mA