Test: Surface Area & Volumes- 2 - Class 9 MCQ

The cost of digging a pit of dimensions 4.5m×2.5m×2.5m at the rate of Rs 20 per cubic metre is

If the volume of a sphere is 4851 cm³, then its surface area is

The lateral surface area of a cube is 256 m² The volume of the cube is

The cost of cementing the inner curved surface of a 14 m deep well of radius 2 m at the rate of Rs 2 per m² is

The ratio of the radii of two spheres whose volumes are in the ratio 64 : 27 is

The volume of resulting cuboid formed when two cubes each of side 6 cm are joined end to end is

A hemispherical bowl is made of steel 0.25 cm thick. If the inner radius of the bowl is 3.25 cm, then the outer curved surface area of the bowl is

The difference between the total surface area of a cube of side 4 cm and its lateral surface area is

The diameter of the base of a cylinder of curved surface area 88 cm² and height 14 cm is

Given that the surface area of a spherical shot put is 616 cm². its diameter is

The number of litres that a cuboidal water tank of dimensions 6m×5m×4.5m can hold is

If the surface area of a solid sphere is 1386 cm². then the total surface area of the solid hemisphere of the same radius is

The volume of a cube whose diagonal is 8√3 cm is

The total surface area of a right circular cylinder of height 4 cm and radius 3 cm is

If a spherical balloon grows to twice its radius when inflated, then the ratio of the volume of the inflated balloon to the original balloon is

The surface area of a cuboid whose length, breadth and height are 15 cm, 10 cm and 20 cm respectively is

The number of spherical bullets each 5 dm in diameter which can be cast from a rectangular block of lead 11 m long, 10 m broad and 5 high is

The number of planks of dimensions (5m×25cm×10cm) that can be placed in a pit which is 20 m long, 6 m wide and 80 cm deep is

If the lateral surface area of a cylinder is 132 cm² and its height is 7 cm, then its base diameter is

If the total surface area of a hemisphere is 1848 cm², then the diameter is

The volume of a cylinder whose circumference of the base is 132 cm and height 25 cm is

The number of solid sphere each 6 cm in diameter, which can be moulded from a solid cylinder of height 45 cm and diameter 4 cm without any loss is
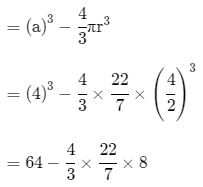
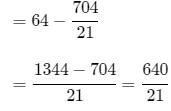