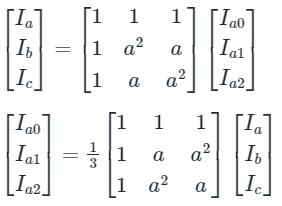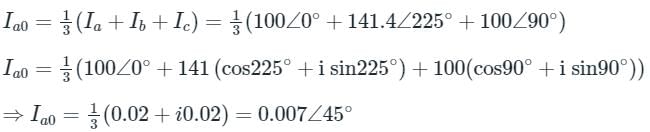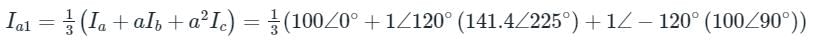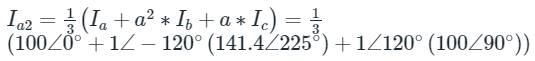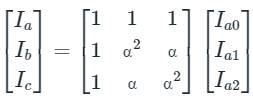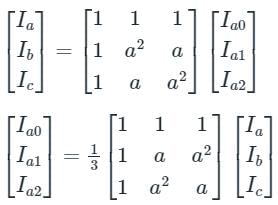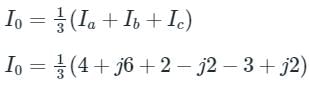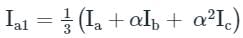Test: Symmetrical Components - 1 - Electrical Engineering (EE) MCQ
12 Questions MCQ Test GATE Electrical Engineering (EE) Mock Test Series 2026 - Test: Symmetrical Components - 1
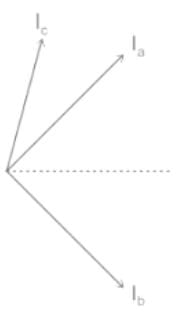
The line current flowing in the lines toward a balanced load connected in delta are Ia = 100∠0°, Ib = 141.4∠225°, Ic = 100∠90°. Find the symmetrical component of the line current.
The series impedance matrix of a short three-phase transmission line in phase coordinates is  . If the positive sequence impedance is (1 + j 10) Ω, and the zero sequence is (4 + j 31) Ω, then the imaginary part of Zm (in Ω) is _______ (up to 2 decimal places).
. If the positive sequence impedance is (1 + j 10) Ω, and the zero sequence is (4 + j 31) Ω, then the imaginary part of Zm (in Ω) is _______ (up to 2 decimal places).
 . If the positive sequence impedance is (1 + j 10) Ω, and the zero sequence is (4 + j 31) Ω, then the imaginary part of Zm (in Ω) is _______ (up to 2 decimal places).
. If the positive sequence impedance is (1 + j 10) Ω, and the zero sequence is (4 + j 31) Ω, then the imaginary part of Zm (in Ω) is _______ (up to 2 decimal places).In an unbalanced three phase system, phase current Ia = 1∠(-90°) pu, negative sequence current Ib2 = 4 ∠(-150°) pu, zero sequence current IC0 = 3∠ 90° pu. The magnitude of phase current Ib in pu is
Symmetrical components are used in power system for the analysis of
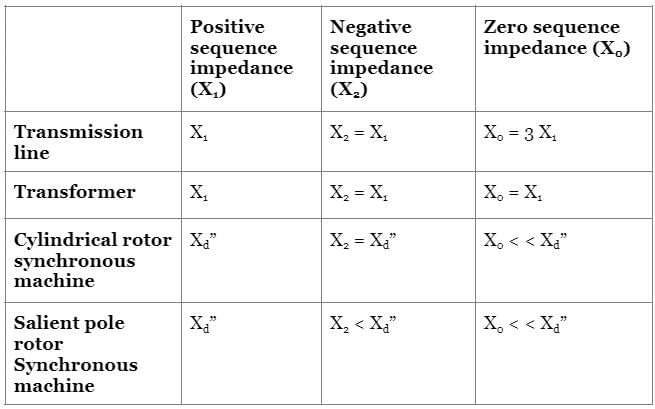
For which of the following element the positive, negative and zero sequence impedances are equal
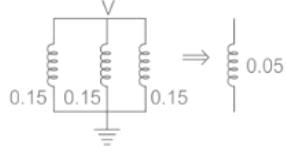
Three synchronous generators, each of which is rated to 100 MVA, 11 KV, have an impedance per unit of 0.15. If all three generators are replaced by a single equivalent generator, what will be the effective per unit impedance of each generator?
The line current in a three phase unbalanced load are Ia = 4 + j6, Ib = 2 - j2, Ic = -3 + j2, then zero sequence component of current will be
The zero-sequence current of a generator for line to ground fault is j2.4 pu. The current through neutral during the fault is -
If the positive, negative and zero-sequence reactance of an element of a power system are 0.3, 0.3 and 0.8 p.u. respectively, then the element would be a?
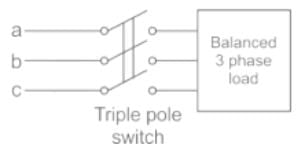
A balanced 3-phase load is supplied from a 3-phase supply. The contact in line c of the triple pole switch contactor fails to connect when switched on. If the line currents in lines a and b record 25A each, then the positive sequence component of the current is
Suppose IA, IB and IC are a set of unbalanced current phasors in a three-phase system. The phase-B zero-sequence current IB0 = 0.1 ∠0° p.u. If phase-A current IA = 1.1 ∠0° p.u. and phase-C current IC = (1 ∠120° + 0.1) p.u. then IB in p.u. is
|
26 docs|257 tests
|
|
26 docs|257 tests
|