Test: The Continuous, Time Fourier Series & The Discrete, Time Fourier Transform - Electronics and Communication Engineering (ECE) MCQ
15 Questions MCQ Test - Test: The Continuous, Time Fourier Series & The Discrete, Time Fourier Transform
Determine the Fourier series coefficient for given periodic signal x(t).
Que: x(t) as shown in fig.
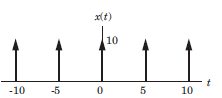
Determine the Fourier series coefficient for given periodic signal x(t).
Que: x(t) as shown in fig.
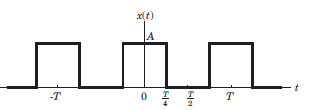
Determine the Fourier series coefficient for given periodic signal x(t).
Que: x(t) as shown in fig.
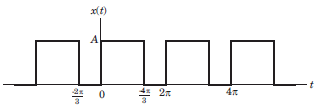
Determine the Fourier series coefficient for given periodic signal x(t).
Que: x(t) as shown in fig.
Determine the Fourier series coefficient for given periodic signal x(t).
x(t) = sin2t
In the question, the FS coefficient of time-domain signal have been given. Determine the corresponding time domain signal and choose correct option.
In the question, the FS coefficient of time-domain signal have been given. Determine the corresponding time domain signal and choose correct option.
In the question, the FS coefficient of time-domain signal have been given. Determine the corresponding time domain signal and choose correct option.
Que: X[k] as shown in fig, wo = π
In the question, the FS coefficient of time-domain signal have been given. Determine the corresponding time domain signal and choose correct option.
Que: X[k] As shown in fig. , ωo = 2π
In the question, the FS coefficient of time-domain signal have been given. Determine the corresponding time domain signal and choose correct option.
Que: X[k] As shown in fig. , ωo = π
Consider a continuous time periodic signal x(t) with fundamental period T and Fourier series coefficients X[k]. Determine the Fourier series coefficient of the signal y(t) given in question and choose correct option.
Que: y(t) = x(t - t0 ) + x (t + t0 )
Consider a continuous time periodic signal x(t) with fundamental period T and Fourier series coefficients X[k]. Determine the Fourier series coefficient of the signal y(t) given in question and choose correct option.
Que: y(t) = Ev{x(t)}
Consider a continuous time periodic signal x(t) with fundamental period T and Fourier series coefficients X[k]. Determine the Fourier series coefficient of the signal y(t) given in question and choose correct option.
Que: y(t) = Re{x(t)}
Determine the signal having the Fourier transform given in question.
Determine the signal having the Fourier transform given in question.














