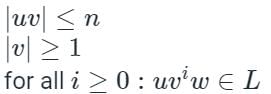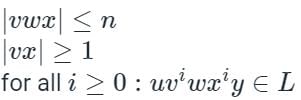Test: Theory of Computation - 1 - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test GATE Computer Science Engineering(CSE) 2026 Mock Test Series - Test: Theory of Computation - 1
Which of the following is sufficient to convert an arbitrary Context Free Grammar (CFG) to an LL(1) grammar?
Which of the following languages accept pumping lemma?
Which of the following languages is generated by the given grammar?
S → aS | bS | ϵ
S → aS | bS | ϵ
Identify the language generated by the following grammar, where S is the start variable.
S → XY
X → aX | a
Y → aYb | ϵ
Language L1 is defined by the grammar: S1 → aS1b|ϵ
Language L2 is defined by the grammar: S2 → abS2|ϵ
Consider the following statements:
P: L1 is regular
Q: L2 is regular
Which one of the following is TRUE?
Consider the language L = {an |n ≥ 0} ∪ {anbn| n ≥ 0} and the following statements.
I. L is deterministic context-free.
II. L is context-free but not deterministic context-free.
III. L is not LL(k) for any k.
Which of the above statements is/are TRUE?
Consider the following statements.
I. If L1 ∪ L2 is regular, then both L1 and L2 must be regular.
II. The class of regular languages is closed under infinite union.
Which of the above statements is/are TRUE?
For Σ = {a, b}, let us consider the regular language L = {x|x = a2+3k or x = b10+12k k ≥ 0}.
Which one of the following can be a pumping length (the constant guaranteed by the pumping lemma) for L?
Assume the R is a relation on a set A, aRb is partially ordered such that a and b are _____________
A regular language over an alphabet ∑ is one that cannot be obtained from the basic languages using the operation
|
57 docs|215 tests
|
|
57 docs|215 tests
|