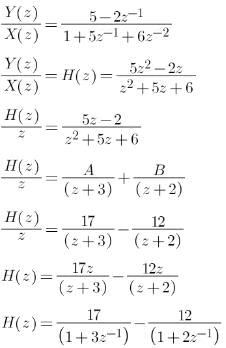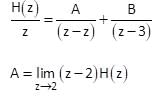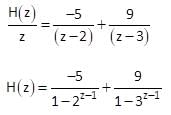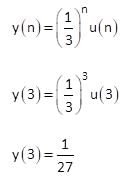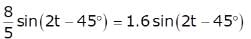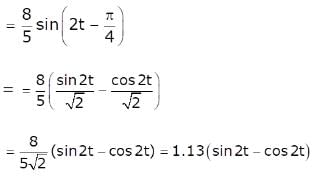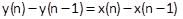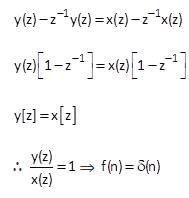Test: Time Scaling, Linear Time Invariant & Casual Systems - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Time Scaling, Linear Time Invariant & Casual Systems
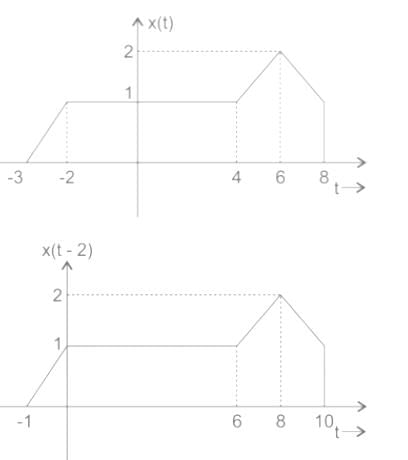
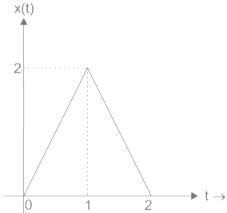
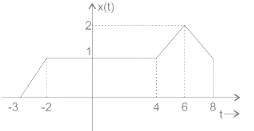
x(t) is shown in figure below. Then x(t) is

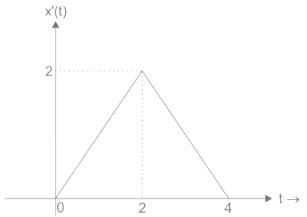
If x(t) is shown below, then what is x(10t - 2)?

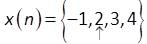 and
and 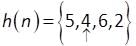
Find y(n) = x (n) ⨂ h(n), where ⨂ denotes circular convolution.
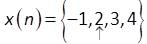 and
and 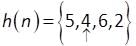
A causal discrete time LTI system is described by:
Y(n) + 5y(n-1) + 6y(n – 2) = 5x(n) – 2x(n-1)
Find the impulse response h(n) of causal system.
Consider an LTI system is such that

h1(n) = δ(n) – 5 δ (n – 1)
h2(n) = 5n u(n)
Find the output of signal at n = 3 for applied input is 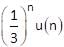
Signal 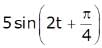 acts as an input for system having impulse response
acts as an input for system having impulse response 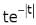 , output of the system is given b
, output of the system is given b
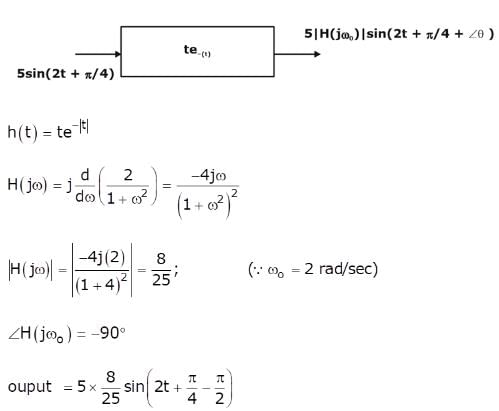
The unit impulse response of the system described by is:
For the system, y (t) = x (t - 5) – x (3 - t) which of the following holds true?
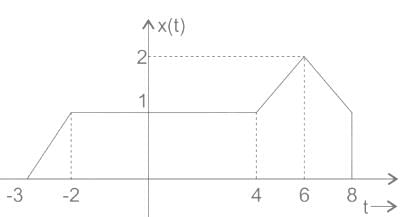
If x(t) is shown above, then what is x(10t - 2)?
Consider the following statements for continuous-time linear time invariant (LTI) systems.
I. There is no bounded input bounded output (BIBO) stable system with a pole in the right half of the complex plane.
II. There is no causal and BIBO stable system with a pole in the right half of the complex plane.
Which one among the following is correct?