Test: Triangles- Assertion-Reason & Case Base Type Questions - Class 9 MCQ
6 Questions MCQ Test - Test: Triangles- Assertion-Reason & Case Base Type Questions
Direction: A children‘s park is in the shape of isosceles triangle said PQR with PQ = PR, S and T are points on QR such that QT = RS.
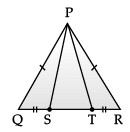
Q. Which rule is applied to prove that congruency of ΔPQS and ΔPRT.

Direction: A children‘s park is in the shape of isosceles triangle said PQR with PQ = PR, S and T are points on QR such that QT = RS.
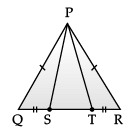
Q. If ∠QPR = 80°. find ∠PQR?

Direction: A children‘s park is in the shape of isosceles triangle said PQR with PQ = PR, S and T are points on QR such that QT = RS.
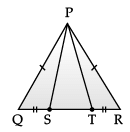
Q. In RHS rule ‘H‘ stands for :

Direction: A children‘s park is in the shape of isosceles triangle said PQR with PQ = PR, S and T are points on QR such that QT = RS.
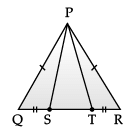
Q. An isosceles triangle has
Direction: A children‘s park is in the shape of isosceles triangle said PQR with PQ = PR, S and T are points on QR such that QT = RS.
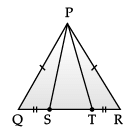
Q. If PQ = 6 cm and QR = 7 cm, then perimeter of ΔPQR is :
Direction: Assertion
Statement 1: In triangle ABC, the centroid (G) divides the line joining orthocentre (O) and circumcentre (C) in ratio 2 : 1.
Reason
Statement 2: The centroid (G) divides the median AD in ratio 2 : 1. Select the correct














