Test: Vector Calculus - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Vector Calculus
Given the vector A = (cos x)(cos y)âx + (cos x)(cos y) ây, âx & ây denote unit vectors along x,y directions respectively. The curl of A is ________.
The following surface integral is to be evaluated over a sphere for the given steady vector field, F = xi + yj + zk defined with respect to a Cartesian coordinate system having i, j, and k as unit base vectors.
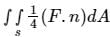 , Where S is the sphere, x2 + y2 + z2 = 1 and n is the outward unit normal vector to the sphere. The value of the surface integral is
, Where S is the sphere, x2 + y2 + z2 = 1 and n is the outward unit normal vector to the sphere. The value of the surface integral is
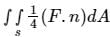 , Where S is the sphere, x2 + y2 + z2 = 1 and n is the outward unit normal vector to the sphere. The value of the surface integral is
, Where S is the sphere, x2 + y2 + z2 = 1 and n is the outward unit normal vector to the sphere. The value of the surface integral isFor the curve xy3 - yx3 = 6, the slope of the tangent line at the point (1, -1) is:
The parabolic arc y = √x, 1 ≤ x ≤ 2 is revolved around the x-axis. The volume of the solid of revolution is
The value of the line integral
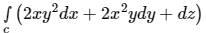
along a path joining the origin and the point (1,1,1) is
The volume determined from ∫∫∫v 8 xyz dv for V = [2, 3] × [1, 2] × [ 0,1 ] will be (in integer) ________.
If 2î + 4ĵ - 5k̂ and î + 2ĵ + 3k̂ are two different sides of rhombus. Find the length of diagonals.
The vector function expressed by
F = ax(5y − k1z) + ay(3z + k2x) + az(k3y−4x)
Represents a conservative field, where ax, ay, az are unit vectors along x, y and z directions, respectively. The values of constant k1, k2, k3 are given by:
The value of  from A(a, 0, 0) to B(a, 0, 2π b) along r̅ = (a cos t) î + (a sin t) ĵ + b t k̂ is:
from A(a, 0, 0) to B(a, 0, 2π b) along r̅ = (a cos t) î + (a sin t) ĵ + b t k̂ is:


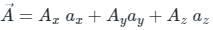
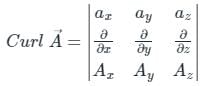
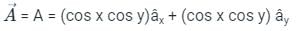
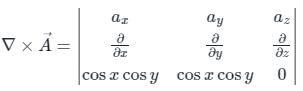
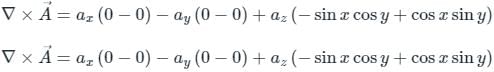
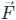 taken over a closed surface ‘S’ is equal to the volume integral of the divergence of that vector function
taken over a closed surface ‘S’ is equal to the volume integral of the divergence of that vector function 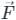 taken over a volume enclosed by the closed surface ‘S’.
taken over a volume enclosed by the closed surface ‘S’.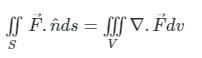
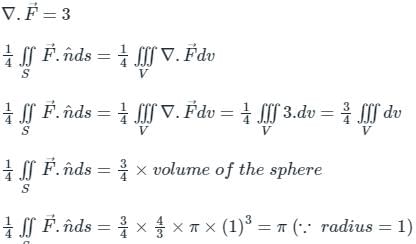

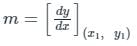
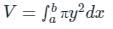
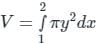
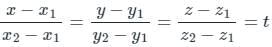

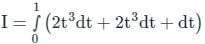
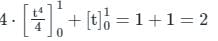
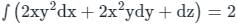
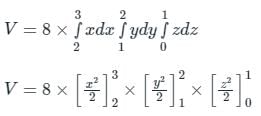
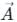 = aî+bĵ+ck̂ and B =
= aî+bĵ+ck̂ and B = 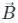 = pî+qĵ+rk̂
= pî+qĵ+rk̂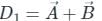
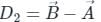
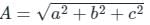
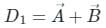
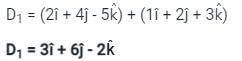

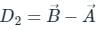
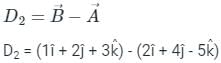
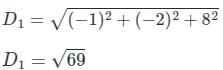
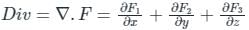
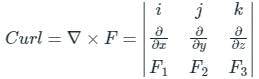
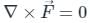 (or) Null Vector.
(or) Null Vector.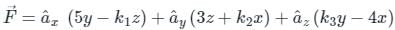 is a conservative field.
is a conservative field.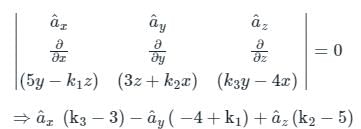
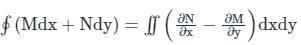
 From A(a, 0, 0) to B(a, 0, 2π b) along r̅ = (a cos t) î + (a sin t) ĵ + b t k̂ is: πa (bĵ + ak̂)
From A(a, 0, 0) to B(a, 0, 2π b) along r̅ = (a cos t) î + (a sin t) ĵ + b t k̂ is: πa (bĵ + ak̂)










