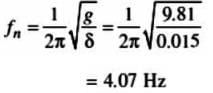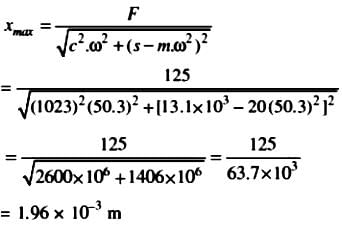Theory of Machines & Vibrations - 2 - Mechanical Engineering MCQ
20 Questions MCQ Test - Theory of Machines & Vibrations - 2
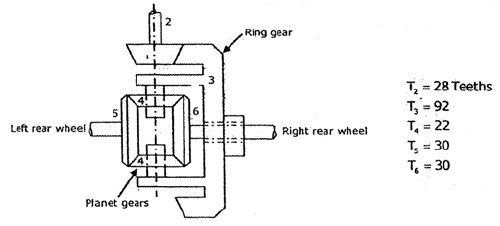
The differential for a rear of driven vehicle is shown below. If the drive shaft turns 1000 rpm, then calculate the speed of the vehicle such that wheel does not slip. Take outside diameter of the wheels as 1 m.
In a four bar linkage mechanism, the input link has a radius of 25 cm and torque of 100 N.m, the output link has a length of 70 cm and a torque of 250 N.m. The mechanical advantage of the four bar linkage is
To transmit energy of 10000 N.m with 5% coefficient of fluctuation, calculate mass moment of inertia of the system. The maximum and minimum fluctuation of energies is 750 Nm and 250 Nm respectively.
Match the following
Section – A
a. S + L < P + Q
b. S + L = P + Q
c. S + L > P + Q
Section – B
1. Grashoff class – I type
2. Kutzbach class – I type
3. Grashoff class – II type
4. Kutzbach class – II type
5. Kutzbach class – III type
6. Grashoff class – III type
The mobility of the following linkage system is
A body of mass 20 kg is suspended from a spring which deflects 15 mm under this load. Calculate the frequency of free vibrations and verify that a viscous damping force amounting to approximately 1000 N at a speed of 1 m/s is just-sufficient to make the motion aperiodic. If when damped to this extent, the body is subjected to a disturbing force with a maximum value of 125 N making 8 cycles/s, find the amplitude of the ultimate motion.
Match the following
List – I
P. Ratio of force transmitted to force applied
R. Damping force per unit velocity
List – II
1. Dimpling coefficient
2. Damping factor
3. Magnification factor
4. Logarithmic decrement
5. Transmissibility ratio
A simply supported shaft of 20 mm diameter and 0.6 m long carries a mass of 1 kg at its mid point. The density of the shaft is 40 × 103 kg/m3 and Young’s modulus of the shaft is 200 GPa. The critical speed of the shaft is __________ rpm.
The measurements on a mechanical vibrating system show that it has a mass of 10 kg and that the springs can be combined to give an equivalent stiffness of the springs 6 N/mm. The dashpot is attached to the system which exerts a force of 40 N when the mass has a velocity of 1 m/s
Q. Determine the damping factor
The measurements on a mechanical vibrating system show that it has a mass of 10 kg and that the springs can be combined to give an equivalent stiffness of the springs 6 N/mm. The dashpot is attached to the system which exerts a force of 40 N when the mass has a velocity of 1 m/s
Q. Determine the logarithmic decrement
The degree of the freedom for the figure shown below is
A punching machine punches 3.8 cm diameter holes in a 3.2 cm thick plate and does 1000 J of work per square cm of sheared area. The punch has a stroke of 15 cm and punches 10 holes per minute. The energy required per punch is
An assemble of links and joints, interconnected in a way to provide a controlled output motion in response to a supplied input motion is defined as
A diameteral pitch of 6cm, 20° pressure angle, 19-tooth pinion is meshed with a 37-tooth gear. Determine the base pitch measured on the base circle.
Match the following
Section – A
a. Belt and rope drive with slip
b. Belt and rope drive without slip
c. Length of tooth parallel to gear axis
d. Watts indicator mechanism
Section – B
1. Face
2. Face width
3. Higher pair
4. Lower pair
5. Double crank mechanism
6. Double lever mechanism
If damping coefficient and critical damping coefficient of a vibrating system are 40N/m/s and 416 N/m/s respectively, then the logarithmic decrement is _______.
The two gear tooth 80 (pinion) and 30 (gear) are in contact with each other. The path of approach between the gears is 120 mm and path of recess is 80 mm. The angular velocity and diameter of pinion is 20 rad/s and 100 mm respectively.
Q. Determine the ratio of sliding velocity to rolling velocity at the beginning of contact.
The two gear tooth 80 (pinion) and 30 (gear) are in contact with each other. The path of approach between the gears is 120 mm and path of recess is 80 mm. The angular velocity and diameter of pinion is 20 rad/s and 100 mm respectively.
Q. Determine the ratio of sliding velocity to rolling velocity at the pitch point.
In an epicyclic gear train with a sun gear, planet gear and a moving arm. The ratio of number of teeth of the sun gear to that of the planet gear is 3. If the planet gear is fixed and the arm has an angular velocity of 150 RPM, the sun gear will rotate with ________ RPM.