UP PGT Math Mock Test - 3 - UPTET MCQ
30 Questions MCQ Test UP PGT Mock Test Series 2025 - UP PGT Math Mock Test - 3
The number of solutions of the equation sin-1 x - cos-1 x = sin-1(1/2) is
If z2 + z + 1 = 0, where z is a complex number, then value of
A card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn and are found to be both diamonds. Find the probability that the lost card was a diamond:
The area bounded by the parabola y = x2 + 1 and the straight line x + y = 3 is given by
How many numbers are there between 100 and 1000, in which all the digits are distinct?
In the vector form, equation of a plane which is at a distance d from the origin, and is the unit vector normal to the plane through the origin is
The number of elements in the Power set P(S) of the set S = {{Φ}, 1, {2, 3}} is
Let R be the relation in the set N given by R = {(a, b): a = b – 2, b > 6}. Choose the correct answer.
Three critics review a book. Odds in favour of book are 5 : 2, 4 : 3 and 3 : 4, respectively for the three critics. The probability that majority are in favour of the book is
Area of triangle formed by tangent to the hyperbola xy = 16 at (16, 1) and co-ordinate axes equals
If P and Q are the points of intersection of the circles x2 + y2 + 3x + 7y + 2p - 5 = 0 and x2 + y2 + 2x + 2y - p2 = 0 , then there is a circle passing through P, Q and (1, 1) for
Let a > 0, b > 0 and c > 0. Then both the roots of the equation ax2 + bx + c = 0
The third term of a G.P. is 4. The product of the first five terms is
Two cards are drawn one at a time & without replacement from a pack of 52 cards. Determine the number of ways in which the two cards can be drawn in a definite order.
If n(A) = 3, n(B) = 6 and A ⊆ B. Then the number of elements in A ∪ B is equal to:
If f(x) = x2 and g(x) = x are two functions from R to R then f(g(2)) is:
Tangents to the curve y = x3 at the points (1, 1) and (– 1, – 1) are
The point of intersection of the tangents at the point P on the ellipse +
= 1, and its corresponding point Q on the auxiliary circle meet on the line
Let R be the relation over the set of straight lines of a plane such that l1 R l2 ⇔ l1 ⊥ l2. Then, R is
If α, β are the roots of x2 + ax - b = 0 and γ,δ are the roots of x2 + ax + b = 0 then (α - γ) (α - δ) (β - δ) (β - γ) =
Four visitors A, B, C & D arrive at a town which has 5 hotels. In how many ways can they disperse themselves among 5 hotels, if 4 hotels are used to accommodate them.
If A and B are any two square matrices of the same order, then
The 10th term of an G.P. is and the 5th term is
.What is the Common Ratio?
|
30 tests
|


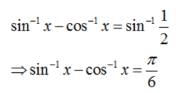
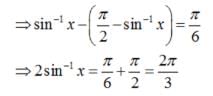
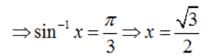
 is
is
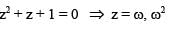
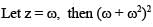
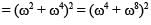
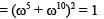
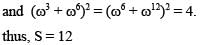

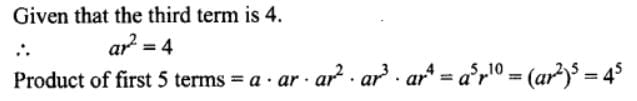
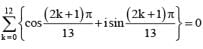



 , then A-1 exists if
, then A-1 exists if