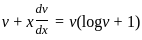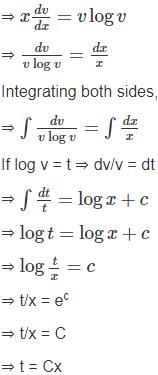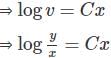UP TGT Mathematics Mock Test - 1 - UPTET MCQ
30 Questions MCQ Test UP TGT Exam Mock Test Series 2025 - UP TGT Mathematics Mock Test - 1
Consider the following pairs:
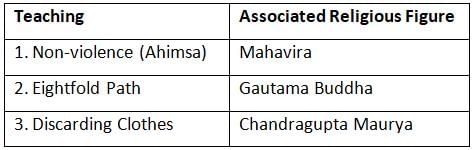
How many of the above pairs are correctly matched?

How many of the above pairs are correctly matched?
Given that A is a square matrix of order 3 and |A| = -2 then the determinant of A-1 is .
If 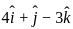 and
and 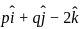 are collinear vectors, then what are the possible values of p and q respectively?
are collinear vectors, then what are the possible values of p and q respectively?
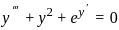 are_____
are_____
Which of the following values is/are correct in terms of vector multiplication?
The number of common tangents to the circles x2 + y2 - 6x - 14y + 48 = 0 and x2 + y2 - 6x = 0 is:
Which among the following is a Skew-symmetric matrix?
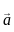 and
and 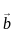 respectively, then the position vector of mid-point of AB is:
respectively, then the position vector of mid-point of AB is:
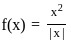 for x ≠ 0 and f(0) = 0?
for x ≠ 0 and f(0) = 0?
In the given figure AOB is a quadrant of a circle where PT = 96 cm, PB = 36 cm, OT = r. Find radius of the circle.
The curve represented by the equations
x = 3(cost + sint)
y = 4(cost - sint) is
Equation of the hyperbola with eccentricity 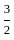 and foci at (± 2, 0) is 5x2 - 4y2 = k2. What is the value of k?
and foci at (± 2, 0) is 5x2 - 4y2 = k2. What is the value of k?
In a triangle ABC, sin A - cos B - cos C = 0. What is angle B equal to?
The maximum value of 3 cos θ + 5 sin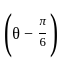 for any real value of θ is
for any real value of θ is
Find the projection of the vector 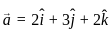 on the vector
on the vector  ?
?
In an equilateral ΔABC, BF ⊥ AC and FE ⊥ BC, then find the ratio of ar Δ ABC to the ar ΔFEC.
If 1, ω, ω2 are the cube roots of unity, then the value of
(1 + ω2)(1 + ω4)(1 + ω8)(1 + ω16) is



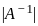 =
= 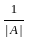
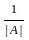
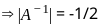
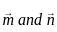 to be collinear,
to be collinear,  where λ is a scalar.
where λ is a scalar.

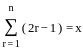 then
then 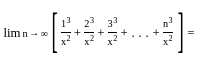
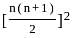
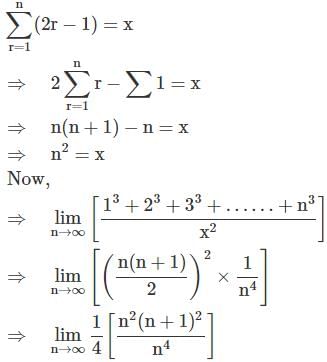
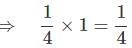
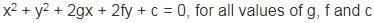
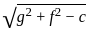
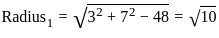
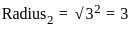
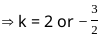
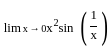
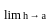
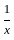
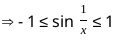
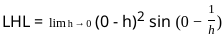
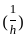

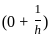
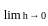
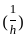

 and
and 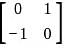 are Skew-symmetric matrix.
are Skew-symmetric matrix.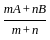
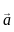
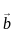
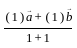
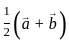
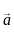
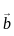
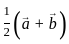
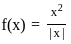
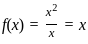

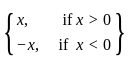
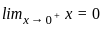
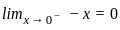
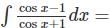
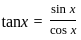
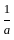 tan ax + C
tan ax + C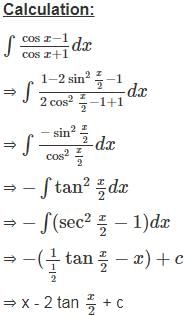
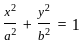
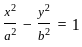
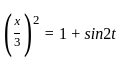 ----(1)
----(1)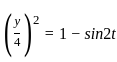 ----(2)
----(2)
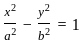

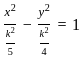
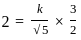
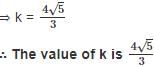
 ) cos(
) cos( )
) ) cos(
) cos(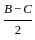 )
) ) cos(
) cos(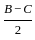 )
)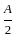 ) cos(
) cos(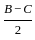 )
)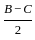 )
) .
.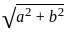
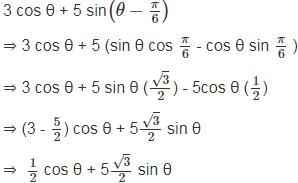
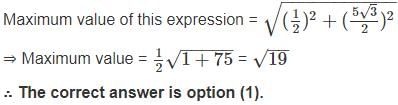
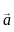 on other vector
on other vector 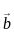 is given by:
is given by: 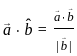
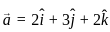 and
and 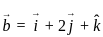
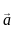 on other vector
on other vector 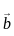 is given by:
is given by: 
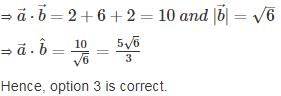
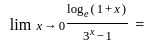
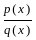 such that,
such that, 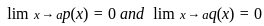 ,
,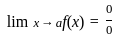 form }
form }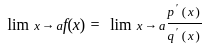

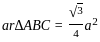
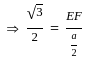
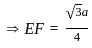
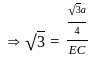
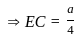
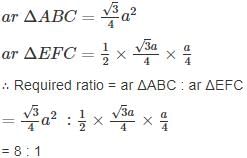
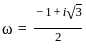
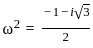
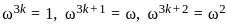
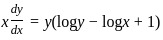 , then the solution of the equation is
, then the solution of the equation is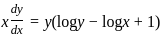
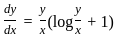 -----(i)
-----(i)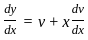
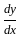 in (i),
in (i),