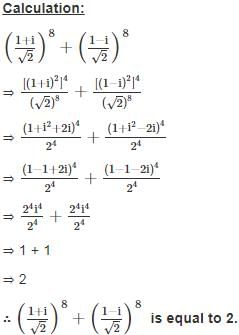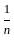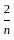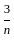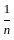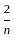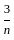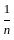UP TGT Mathematics Mock Test - 5 - UPTET MCQ
30 Questions MCQ Test UP TGT Exam Mock Test Series 2025 - UP TGT Mathematics Mock Test - 5
Consider the following statements:
- The Kingdom of Anga was initially a powerful neighbor of Magadha before being conquered by Bimbisara.
- Avanti, with its capital at Ujjain, was a significant competitor to Magadha due to its rich iron deposits.
- The economic prosperity of Magadha was largely dependent on its agricultural productivity, which was negligible compared to its trade and commerce.
How many of the statements given above are correct?
Which one of the following sources informed us about the division of Indian society into seven castes?
Which of the following poets (who adomed the court of Krishnadeva Raya) is known all over southern India for his wit and humour?
Who wrote the history of Aurangazeb’s reign in total secrecy because of the emperor’s oppositon to it?
Which country's aerospace and defence company set up an Indian subsidiary named AeroSpace Services India (ASI)?
If mean of the observations 25, 29, 25, 32, 24 and x is 27, then median of the observations is
The number of solution of the given equation tanθ + secθ = √3, where 0 < θ < 2π is
The rule of combination of a set G of elements e, a, b, c under an operation * is displayed in the adjoining operation table. Then for the group (G, *), the true statement is:

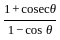
In the given figure, ABCD is a rhombus in which ∠OCB = 60° . Then, find the value of AC : BD.
An ellipse, with foci at (0, 2) and (0, -2) and minor axis of length 4, passes through which of the following points
MA and MB are two tangents from a point M outside the circle with centre O. If A and B are points on the circle such that ∠AMB = 110°, then find the value of ∠OAB?
If the position vectors of the points A, B, C are î + ĵ, î - ĵ and aî + bĵ + ck̂ respectively, then the points A, B, C are collinear if
 ) + (1 -
) + (1 - 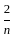 ) + (1 -
) + (1 - 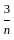 ) + up to n term will result as:
) + up to n term will result as:



 term
term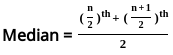 term
term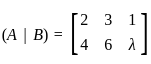
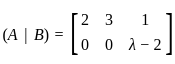
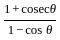
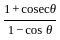
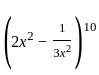 is
is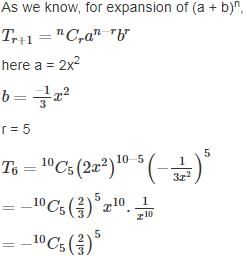
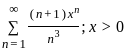
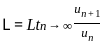
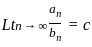
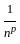 is convergent for p > 1 and divergent for p ≤ 1
is convergent for p > 1 and divergent for p ≤ 1 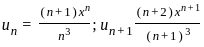

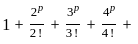 ______, is convergent
______, is convergent 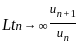
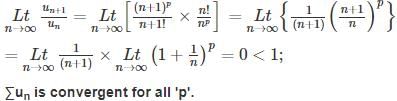

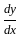 at
at 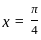 is
is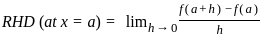
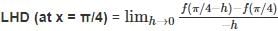
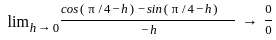


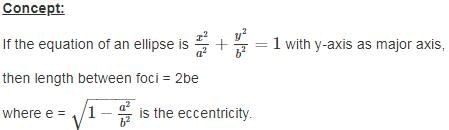

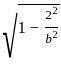 = 4
= 4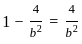

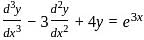 is
is


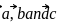 are collinear if and only if the vectors
are collinear if and only if the vectors 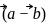 and
and 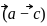 are parallel.
are parallel.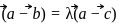

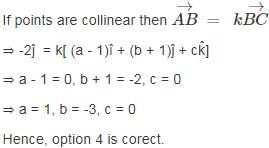

 is equal to
is equal to