VITEEE PCME Mock Test - 2 - JEE MCQ
30 Questions MCQ Test VITEEE: Subject Wise and Full Length MOCK Tests - VITEEE PCME Mock Test - 2
A circle is tangent to the line y = x at the point P(1, 1) and passes through point (1, -3). Find the radius of the circle.
In the standard form of an ellipse sum of the focal distances of a point on the ellipse is
The curve described parametrically by:
x = t² + 2t - 1,
y = 3t + 5
represents:
If f(x) is a polynomial of least degree such that 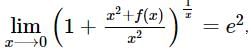 then f(x) =
then f(x) =
If the equation 4y³ - 8a²yx² - 3ay²x + 8x³ = 0 represents three straight lines, two of which are perpendicular, then the sum of all possible values of a is equal to:
If A is a 3×3 non-singular matrix such that AA′ = A′A, and B = A⁻¹A′, then BB′ equals:
The modulus and amplitude of (1 + 2i) / [1 - (1 - i)²] are:
The value of objective function is maximum under linear constraints is
If a, b ∈ R and a ≠ 0, and the quadratic equation ax² − bx + 1 = 0 has imaginary roots, then the value of a + b + 1 is:
A ring, disc and solid sphere are having same speed of COM at the bottom of incline as shown in the figure. If surface of incline is sufficiently rough, the ratio of height attained by ring, disc and sphere is
Energy from the sun is received on earth at the rate of 2 cal per cm2 per min. If average wavelength of solar light be taken as 5500, then how many photons are received on the earth per cm2 per min?
(h = 6.6 x 10-34 Js, 1 cal = 4.2 J).
The current-voltage graph for a device is shown in the figure.

The resistance is negative in the region
Which of the following type of radiations are radiated by an oscillating electric charge?
A typical silt (hard mud) particle of radius 20 μm, whose density is 2000 kg m⁻³, is on the top of a lake. The viscosity and density of lake water are 1.0 mPa and 1000 kg m⁻³, respectively. If the lake is standing still (has no internal fluid motion), the terminal speed with which the particle hits the bottom of the lake is ____ mm s⁻¹.
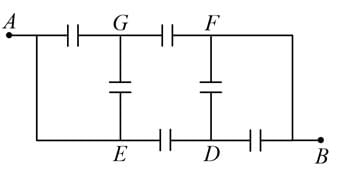
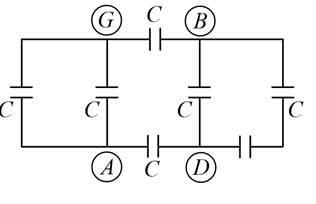
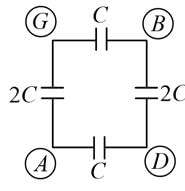
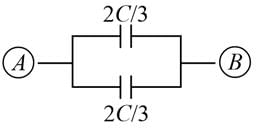
A network of six identical capacitors, each of value C, is made as shown in the figure.
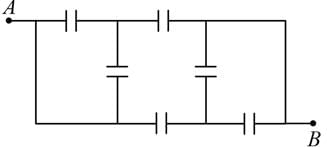
The equivalent capacitance between the points A and B is
Starting from the rest, a body slides down a 45°inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is
When a charged particle moving with velocity 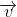 is subjected to a magnetic field of induction
is subjected to a magnetic field of induction 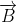 , the force on it is non-zero. This implies that the angle between
, the force on it is non-zero. This implies that the angle between
If the distance between Na+ and CI- ions in sodium chloride crystal is y pm, the length of the edge of the unit cell is
The values of the reduction potentials of Cr3+ and Mn3+ are -0.41V and +1.51V, respectively. Choose the option that is inferred from the given factual information.
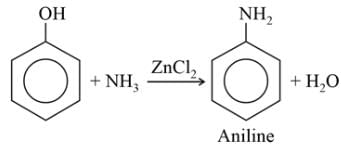
When heated with NH3 under pressure alone or in presence of zinc chloride phenols are converted into
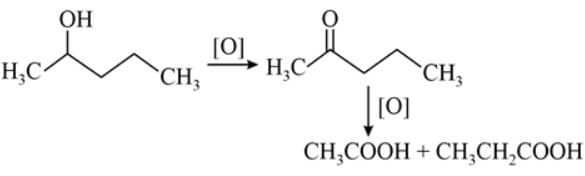
An alcohol on oxidation is found to give CH3COOH and CH3CH2COOH. The structure of the alcohol is
The element, which exhibits both vertical and horizontal similarities are
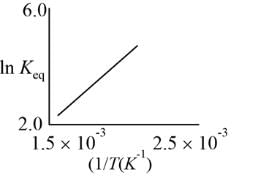
A schematic plot in ln Keq versus inverse of temperature for a reaction is shown below. The reaction must be
Pran and Khan start from their office and walk in opposite directions. Each of them walked for 10 km, after which Khan turns right and walks 15 km. How far are they now from each other?
If we write all the whole numbers from 200 to 400, then how many of these numbers contain the digit 7 exactly once?
|
1 videos|7 docs|63 tests
|
|
1 videos|7 docs|63 tests
|




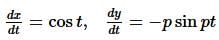
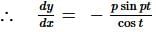
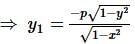
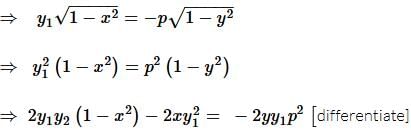

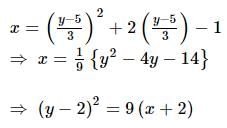
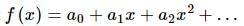
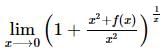 exist only when
exist only when 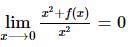
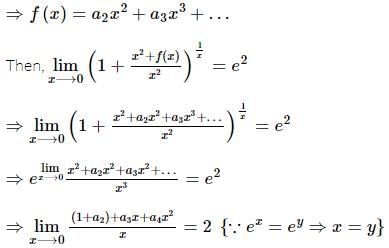
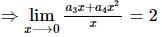
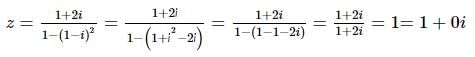
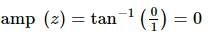

 = 3.6
= 3.6  10–19 J
10–19 J

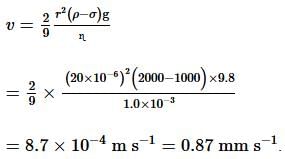
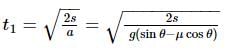
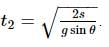
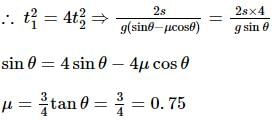
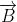 with velocity
with velocity 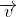 such that angle between
such that angle between 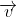 and
and 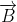 be θ,
be θ,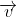 and
and 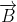 so θ van have any value other than zero and 180°.
so θ van have any value other than zero and 180°. 

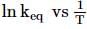 has slope > 0
has slope > 0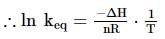
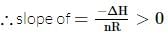
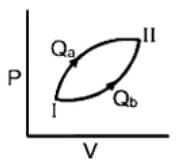
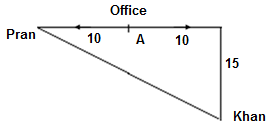
 =
=  =
=  = 25 km
= 25 km










