Vector Calculus - 2 - IIT JAM MCQ
20 Questions MCQ Test - Vector Calculus - 2
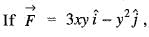 then the value of
then the value of 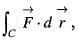 where C is the curve in the XY-plane, y = 2x2 from (0,0) to (1,2) is
where C is the curve in the XY-plane, y = 2x2 from (0,0) to (1,2) is
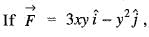 then the value of
then the value of 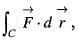 where C is the curve in the XY-plane, y = 2x2 from (0,0) to (1,2) is
where C is the curve in the XY-plane, y = 2x2 from (0,0) to (1,2) isValue of the integral 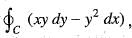 where C is the square cut from the first quadrant by the lines x = 1 and y = 1 will be (use Green’s theorem to change the line integral into double integral)
where C is the square cut from the first quadrant by the lines x = 1 and y = 1 will be (use Green’s theorem to change the line integral into double integral)
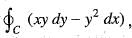 where C is the square cut from the first quadrant by the lines x = 1 and y = 1 will be (use Green’s theorem to change the line integral into double integral)
where C is the square cut from the first quadrant by the lines x = 1 and y = 1 will be (use Green’s theorem to change the line integral into double integral)The directional derivative of f(x, y, z) = x2 + y2 + z2 at the point (1, 1, 1) in the direction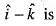
The unit normal vector to the surface of the sphere x2 + y2 + z2 = 1 at the point 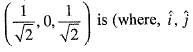 and
and 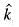 are unit normal vectors in the Cartesian coordinate system)
are unit normal vectors in the Cartesian coordinate system)
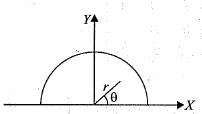
Apply Green’s theorem the value of  where C is the boundary of the area enclosed by the X-axis and the upper half of the circle x2 + y2 = a2 is
where C is the boundary of the area enclosed by the X-axis and the upper half of the circle x2 + y2 = a2 is
Unit vectors in X and Z-directions are 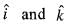 respectively. Which one of the following is the directional derivative of the function F(x, z) = In (x2 + z2) at the point P(4, 0), in the direction of
respectively. Which one of the following is the directional derivative of the function F(x, z) = In (x2 + z2) at the point P(4, 0), in the direction of 
For a scalar function f(x, y, z) = x2 + 3y2 + 2z2, the gradient at the point P(1, 2, -1) is
The value of α for which the following three vectors are coplanar is 
Apply Green’ s theorem the value of 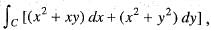 where C is the square formed by the lines y = ±1, x = ±1 is
where C is the square formed by the lines y = ±1, x = ±1 is
The divergence of the vector field 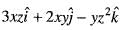 at a point (1, 1, 1) is equal to
at a point (1, 1, 1) is equal to


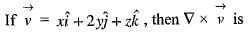
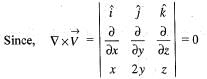



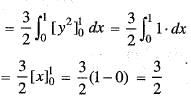

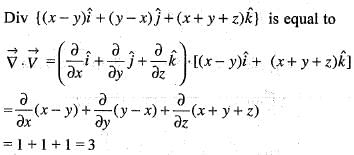
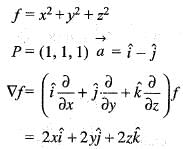
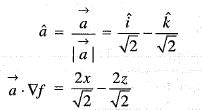
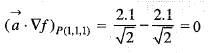
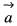 the point P(1, 1, 1),
the point P(1, 1, 1),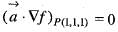
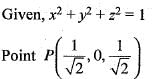
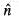 is given by
is given by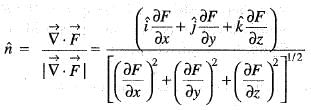
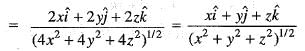
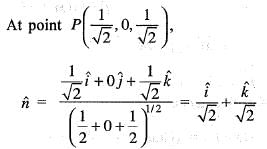
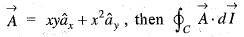 over the path shown in the figure is
over the path shown in the figure is 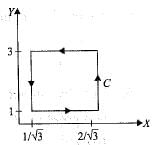

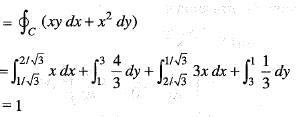
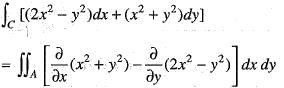
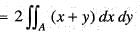
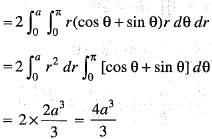
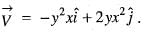 The motion at (x, y) =
The motion at (x, y) = 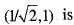
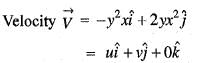
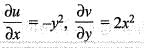
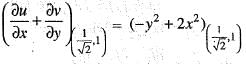
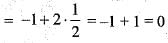


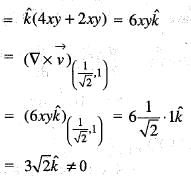
 is rotational and incompressible.
is rotational and incompressible.
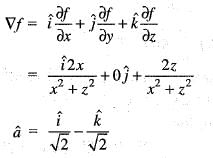
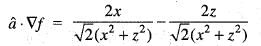
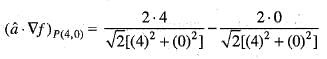
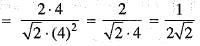
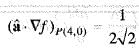

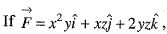 then the value of div Curl
then the value of div Curl 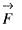 is
is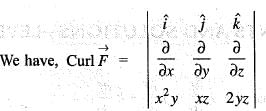
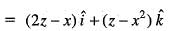
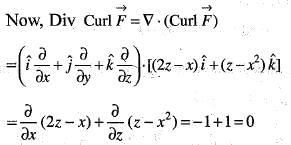

 are coplanar, if
are coplanar, if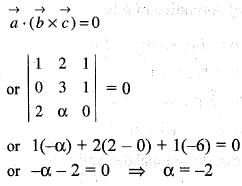
 with
with  we get M = x2 + xy and
we get M = x2 + xy and 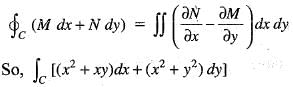
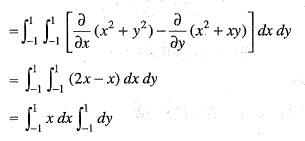
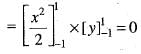

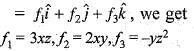
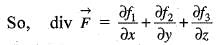
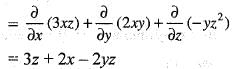
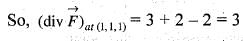
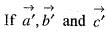 is the reciprocal system to the vectors
is the reciprocal system to the vectors 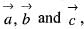 then the value of
then the value of 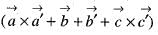
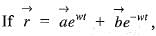 where
where 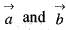 are constant vectors then
are constant vectors then 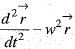 is equal to
is equal to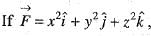 , then the value of div curl
, then the value of div curl 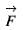 is
is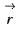 will be
will be










