“गणित विज्ञानों की रानी है और संख्या सिद्धांत गणित की रानी है” यह कथन किसके द्वारा कहा गया है:

बर्नार्ड थॉमस

गणित से संबंधित कौन सा कथन है?

मस्तिष्क का व्यायाम

छात्र का दुश्मन

शक्तिशाली की शक्ति

अकांक्षा एक अच्छी गणित की शिक्षिका बनना चाहती है। एक अच्छी गणित की शिक्षिका बनने के लिए उसे

वास्तविक जीवन की गणित की सामग्री से संबंधित अवधारणात्मक ज्ञान, समझ और क्षमता

अच्छी संचार कौशल और बंद-प्रश्नों का ज्ञान

समस्याओं को तुरंत हल करने की क्षमता

संख्यात्मक प्रणाली, बीजगणित और ज्यामिति का अच्छा ज्ञान।

कक्षा IV के लिए 'समय' के मूल्यांकन के पैरामीटर क्या होंगे?

केवल समान घड़ी पर समय पढ़ना

डिजिटल और समान घड़ी पर समय पढ़ना, आधा, एक चौथाई, एक चौथाई कम, पूर्वाह्न, अपराह्न, मिनट और सेकंड के बीच संबंध का विचार

डिजिटल घड़ी पर समय पढ़ना, केवल पूर्वाह्न और अपराह्न का विचार

केवल डिजिटल घड़ी पर समय पढ़ना

निर्देश: निम्नलिखित प्रश्नों का उत्तर सही/सबसे उपयुक्त विकल्प चुनकर दें। NCF 2005 के अनुसार, स्कूल गणित उस स्थिति में होता है जहाँ:

गणित बच्चों के जीवन के अनुभव का एक हिस्सा है।

बच्चों को सभी अवधारणाओं को दैनिक अभ्यास द्वारा सीखने के लिए मजबूर किया जाता है।

बच्चे श्रोता होते हैं और शिक्षक एक सक्रिय कथाकार होते हैं।

बच्चे सूत्रों के सामूहिक अभ्यास और परीक्षा में प्रदर्शन के दबाव में शामिल होते हैं।

निम्नलिखित प्रकार के कंप्यूटर को आकार के आधार पर किस प्रकार वर्गीकृत किया जाता है।

एनालॉग कंप्यूटर

डिजिटल कंप्यूटर

हाइब्रिड कंप्यूटर

सूक्ष्म कंप्यूटर

निम्नलिखित में से कौन सा नैदानिक पढ़ाई परीक्षण में शामिल नहीं है?

कविता की समझ और सराहना

विभिन्न क्षेत्रों में शब्दावली

वाक्यों का अर्थ

गलत संख्या का नोट करना

किस परीक्षा में छात्रों को कार्य गतिविधियों में संलग्न होना आवश्यक होता है?

मौखिक परीक्षा

व्यावहारिक परीक्षा

लिखित परीक्षा

उद्देश्यात्मक प्रकार की परीक्षा

शिक्षक को अपनी कक्षा में गणितीय वार्तालाप शुरू करना चाहिए क्योंकि

इससे छात्र चर्चा में शामिल होते हैं जबकि शिक्षक उनके गृहकार्य को देख सकता है

भाषा गणितीय समझ में मदद करती है

गणितीय वार्तालाप हाल के शैक्षिक विमर्श में एक प्रमुख शब्द है

बच्चे वैसे भी बात करते हैं। ऐसे वार्तालाप कुछ अधिक उपयोगी होंगे

एक छात्र लिखता है यह छात्र

हमेशा अनुपात के साथ इकाई लिखने में लेखन त्रुटि करता है

इकाई और उनके रूपांतरण का स्पष्ट अवधारणा है

भिन्नों को सही रूप में निम्नतम रूप में घटा सकता है और इकाइयों को सही ढंग से लिख सकता है

इकाइयों, इकाइयों के रूपांतरण, भिन्नों का अवधारणा है लेकिन अनुपात के इकाइयों का नहीं होने का अवधारणा चूक गया है

कक्षा V में 'बिक्री' पर त्योहार के मौसम में 'प्रतिशत' के विषय के दौरान कक्षा में चर्चा शुरू की गई। कक्षा में इस प्रकार की चर्चा

छात्रों को एक-दूसरे की राय सुनने में मदद करता है और उन्हें अपने तर्क प्रस्तुत करने के लिए प्रोत्साहित करता है।

इसे टाला जाना चाहिए क्योंकि यह कक्षा के शोर स्तर को बढ़ाता है और दूसरों को परेशान करता है।

छात्रों को उनके बहस कौशल को बढ़ाने में मदद करता है।

कक्षा में गर्मागर्म बहसें शुरू करता है और कक्षा के माहौल को बिगाड़ देता है।

एक समान स्थिति में कई संबंधों का अवलोकन करते हुए संबंध के सामान्यीकृत कथन पर पहुँचने की तार्किक प्रक्रिया __________ विधि है।

ह्यूरिस्टिक

जब एक बच्चे से पूछा गया 'क्षेत्रफल क्या है?', तो उसने उत्तर दिया लंबाई चौड़ाई। आप बच्चे की क्षेत्रफल की अवधारणा के बारे में समझ के बारे में क्या कह सकते हैं?

बच्चे ने आयत के क्षेत्रफल का उपयोग किसी भी बंद आकृति के क्षेत्रफल के सामान्य विचार के रूप में किया।

बच्चा यह कहने में सही है कि क्षेत्र लंबाई और चौड़ाई है।

बच्चा क्षेत्रफल और परिमाण के अवधारणा के बीच भ्रमित है।

बच्चे को क्षेत्रफल के अवधारणा के बारे में कोई जानकारी नहीं है।

असाइनमेंट को प्रभावी बनाने के लिए, निम्नलिखित में से किसे नहीं माना जाना चाहिए?

असाइनमेंट को प्रेरक और स्पष्ट होना चाहिए, जिससे सभी संदेह और समझ को दूर किया जा सके।

छात्रों और शिक्षकों के बीच कोई बातचीत नहीं होनी चाहिए।

संदर्भ पुस्तकें, पाठ्य पुस्तकें और अन्य शिक्षण-सीखने की सामग्री का हमेशा उपयोग किया जाना चाहिए।

यह एक सहयोगात्मक गतिविधि होनी चाहिए जिसमें शिक्षक और छात्र सक्रिय भाग लेते हैं।

गणित की शिक्षण के उद्देश्य के बारे में क्या गलत है?

यह बच्चे को ज्यामितीय तथ्यों के बीच संबंधों को समझने में सक्षम बनाता है।

यह शिक्षार्थियों को ज्यामितीय अवधारणाओं को समझने में मदद करता है।

यह तार्किक सोच की पृष्ठभूमि प्रदान करता है।

यह तर्क करने की शक्ति को विकसित नहीं करता है।

शैलजा कक्षा VIII की एक प्रतिभाशाली छात्रा है, निम्नलिखित में से कौन सा उसके कौशल को बढ़ाने में सबसे अधिक मदद करेगा

उसकी विषयों से संबंधित परियोजनाओं को विकसित करने में मदद करना

क्लास प्रतिनिधि बनाना

उसे उन्नत अध्ययन के लिए सहायता प्रदान करना

प्रतियोगी परीक्षा के लिए उसे प्रेरित करना

अंकुर को एक मूल्यांकन में रेखीय समीकरणों पर एक शब्द समस्या में शून्य अंक मिले। शिक्षक को पता है कि वह रेखीय समीकरणों को सही ढंग से हल कर सकता है। शिक्षक को उसके रिपोर्ट में क्या टिप्पणी करनी चाहिए?

अंकुर घर पर अध्ययन और अभ्यास नहीं कर रहा है।

अंकुर ने रेखीय समीकरणों की अवधारणा को पूरी तरह से नहीं समझा है।

अंकुर को प्रश्न की भाषा को समझने में समस्या है, हालाँकि वह समीकरणों को हल कर सकता है।

अंकुर में एकाग्रता की कमी है और इसलिए उसे परीक्षा का फोबिया है।

निर्देश: निम्नलिखित प्रश्नों का उत्तर सबसे उपयुक्त विकल्प चुनकर दें। गणित में, प्रारंभिक चरणों में समस्या को हल करने के लिए मौखिक कार्य इतना महत्वपूर्ण क्यों है?

यह पैसे बचाता है

यह कुछ चरणों को छोड़कर समय और प्रयास की बचत करता है

इस तकनीक द्वारा सीखा गया ज्ञान लंबे समय तक संरक्षित रहता है

यह एक बहुत श्रमसाध्य तकनीक है

पीएजेट का मानना था कि सीखना सामाजिक शिक्षा के परिणामस्वरूप होता है और एक गणित शिक्षक जो पीएजेट के सिद्धांत में विश्वास करता है, उसे क्या उपयोग करना चाहिए?

कक्षा में बहुत सारे मैनिपुलेटिव और प्रयोगशाला गतिविधियाँ

समूह परियोजना और समूह चर्चा

विभिन्नीकृत शिक्षण

चाक और बात करने की विधि

यदि एक छात्र 'पांच हजार पचास' को '550' के रूप में लिखता है, तो इसका अर्थ क्या है?

स्थान मान की अवधारणा स्पष्ट नहीं है

संख्याओं का ज्ञान नहीं है

गणित का ज्ञान नहीं है

जोड़ना नहीं जानता

निम्नलिखित में से कौन सी गणित में समस्या समाधान रणनीति नहीं है?

परीक्षण और त्रुटि

चित्र बनाना

पीछे से हल करना

जब अंशों के जोड़ने की शिक्षा देते समय, एक शिक्षक ने निम्नलिखित गलती का सामना किया।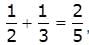 , ऐसी स्थिति में शिक्षक क्या सुधारात्मक कार्रवाई कर सकते हैं?

बच्चे को LCM के सिद्धांत को समझने में मदद करें

बच्चे से कहें कि वह जितना संभव हो सके अभ्यास करे

कोई हस्तक्षेप आवश्यक नहीं है क्योंकि वह बड़े होने पर समझ जाएगी।

बच्चे को प्रत्येक अंश का परिमाण समझने में मदद करें।

“गणित अप्रत्यक्ष मापने का विज्ञान है”, यह कहा गया था

मार्शल एच. स्टोन

शब्द समस्याओं का सामना करते समय, राजन अक्सर पूछता है, 'क्या मुझे जोड़ना चाहिए या घटाना?' 'क्या मुझे गुणा करना चाहिए या भाग करना?'

राजन गुणा नहीं कर सकता।

राजन कक्षा में व्यवधान डालने के अवसरों की तलाश करता है।

राजन को भाषा समझने में समस्या है।

राजन को संख्या संचालन की समझ नहीं है।

अभ्यास परीक्षा: गणित शिक्षा प्रणाली - 3 Free MCQ Practice Test with Solutions

EduRev

Explore Exams

Open App

Important Questions for अभ्यास परीक्षा: गणित शिक्षा प्रणाली - 3

Find all the important questions for अभ्यास परीक्षा: गणित शिक्षा प्रणाली - 3 at EduRev.Get fully prepared for अभ्यास परीक्षा: गणित शिक्षा प्रणाली - 3 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the अभ्यास परीक्षा: गणित शिक्षा प्रणाली - 3 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of अभ्यास परीक्षा: गणित शिक्षा प्रणाली - 3 resources.

अभ्यास परीक्षा: गणित शिक्षा प्रणाली - 3 MCQs with Answers

Prepare for the अभ्यास परीक्षा: गणित शिक्षा प्रणाली - 3 within the CTET & State TET exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for अभ्यास परीक्षा: गणित शिक्षा प्रणाली - 3

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace अभ्यास परीक्षा: गणित शिक्षा प्रणाली - 3 with ease. Join thousands of successful students who have benefited from our trusted online resources.

Education Revolution