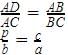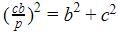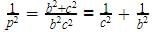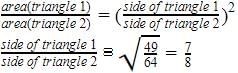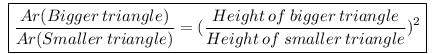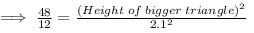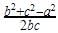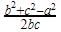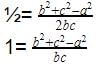आरएस अग्रवाल परीक्षण: त्रिकोण - CTET & State TET MCQ
25 Questions MCQ Test - आरएस अग्रवाल परीक्षण: त्रिकोण
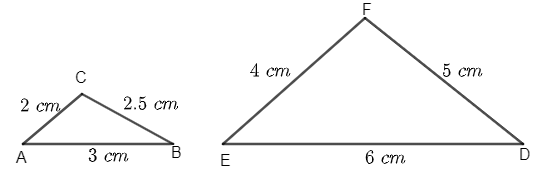
त्रिभुज ABC इस प्रकार है कि AB = 3 सेमी, BC = 2 सेमी और CA = 2.5 सेमी। त्रिभुज DEF त्रिभुज ABC के समान है। यदि EF = 4 सेमी है, तो त्रिभुज DEF का परिमाण क्या होगा:
त्रिकोण ΔABC में, AB = 3 सेमी, AC = 4 सेमी और AD कोण विभाजक है। तब, BD : DC का अनुपात क्या है?
ABC एक त्रिकोण है और DE रेखा BC के समांतर खींची गई है, जो अन्य भुजाओं को D और E पर काटती है। यदि AB = 3.6 सेमी, AC = 2.4 सेमी और AD = 2.1 सेमी है, तो AE के मान के लिए क्या होगा?
त्रिकोण के भुजाओं के मध्य बिन्दुओं को जोड़ने वाली रेखा खंड चार त्रिकोण बनाते हैं, जिनमें से प्रत्येक:
त्रिकोण ΔABC और ΔDEF में, ∠A = 50°, ∠B = 70°, ∠C = 60°, ∠D = 60°, ∠E = 70°, ∠F = 50°, तो ΔABC किसके समान है?
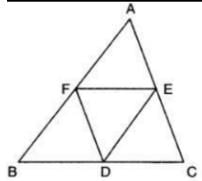
D, E, F त्रिकोण ABC के पक्ष BC, CA और AB के मध्य बिंदु हैं। तब त्रिकोण DEF त्रिकोण ABC के समकक्ष है।
यदि त्रिकोण ABC और DEF में, कोण A कोण E के समान है, दोनों 40° के बराबर हैं, AB : ED = AC : EF है और कोण F 65° है, तो कोण B क्या होगा?
एक समकोण त्रिभुज ΔABC में, जिसमें समकोण A पर है, यदि AD ⊥ BC इस प्रकार है कि AD = p, यदि BC = a, CA = b और AB = c, तब:
संलग्न चित्र में, XY AC के समानांतर है। यदि XY त्रिकोण को समान भागों में विभाजित करता है, तो AX/AB का मान क्या होगा?
दो समान त्रिकोणों के समकक्ष भुजाओं का अनुपात 1 : 3 है। उनके समकक्ष ऊँचाइयों का अनुपात क्या होगा:
दो समान त्रिकोणों का क्षेत्रफल क्रमशः 49 cm2 और 64 cm2 है। उनके संबंधित भुजाओं का अनुपात क्या है?
दो समान त्रिकोणों का क्षेत्रफल 12 सेंटीमीटर2 और 48 सेंटीमीटर2 है। यदि छोटे त्रिकोण की ऊँचाई 2.1 सेंटीमीटर है, तो बड़े त्रिकोण की समकक्ष ऊँचाई:
यदि त्रिकोण ABC में AB, BC और AC त्रिकोण के तीन भुजाएँ हैं, तो निम्नलिखित में से कौन-सी कथन अनिवार्य रूप से सत्य है?
एक त्रिकोण की भुजाएँ क्रमशः 12 सेमी, 8 सेमी और 6 सेमी हैं, यह त्रिकोण किस प्रकार का है?
समभुज त्रिकोण में, इनसेंटर, सर्कमसेंटर, ऑर्थोसेंटर और सेंट्रोइड क्या होते हैं?
सन्निहित चित्र में D, ΔABC के BC का मध्य बिंदु है। DM और DN क्रमशः AB और AC पर लंबवत रेखाएँ हैं और यदि DM = DN है, तो ΔABC है:
त्रिकोण ABC ऐसा है कि AB = 9 सेमी, BC = 6 सेमी, AC = 7.5 सेमी। त्रिकोण ΔDEF त्रिकोण ABC के समान है, यदि EF = 12 सेमी है तो DE कितना है:
त्रिकोण ABC में, AB = 5 सेमी, AC = 7 सेमी। यदि AD कोण A का कोण बाइसेक्टर है। तब BD : CD क्या है?
ΔABC में, D BC का मध्य बिंदु है और E AD का मध्य बिंदु है, BF E के माध्यम से गुजरता है। AF : FC का अनुपात क्या है?
दी गई आकृति में, PS मध्य रेखा है तो ∠QPS क्या होगा?

एक समकोण त्रिकोण की ऊँचाई और आधार के बीच का अंतर 17 सेमी है और इसकी कर्ण 25 सेमी है। त्रिकोण के आधार और ऊँचाई का योग क्या है?
यदि AB, BC और AC त्रिभुज ABC की तीन भुजाएँ हैं, तो निम्नलिखित में से कौन सा सत्य है?
संलग्न आकृति में, D, E और F क्रमशः BC, AC और AB की मध्य बिंदु हैं। ∆DEF त्रिकोण के समान है:
सन्निकटन चित्र में ∠BAC = 60° और BC = a, AC = b और AB = c है, तो: