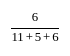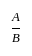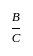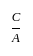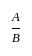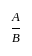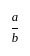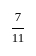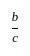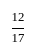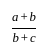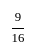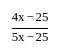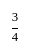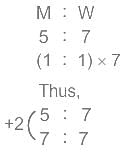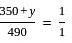Explore Exams
Login Signup
Sign in Open App
CTET & State TET Exam  >  CTET & State TET Tests  >  गणित पत्र 2 (अनुपात और समानुपात) - CTET & State TET MCQ

गणित पत्र 2 (अनुपात और समानुपात) - CTET & State TET MCQ


Test Description

10 Questions MCQ Test - गणित पत्र 2 (अनुपात और समानुपात)

गणित पत्र 2 (अनुपात और समानुपात) for CTET & State TET 2025 is part of CTET & State TET preparation. The गणित पत्र 2 (अनुपात और समानुपात) questions and answers have been prepared according to the CTET & State TET exam syllabus.The गणित पत्र 2 (अनुपात और समानुपात) MCQs are made for CTET & State TET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for गणित पत्र 2 (अनुपात और समानुपात) below.
Solutions of गणित पत्र 2 (अनुपात और समानुपात) questions in English are available as part of our course for CTET & State TET & गणित पत्र 2 (अनुपात और समानुपात) solutions in Hindi for CTET & State TET course. Download more important topics, notes, lectures and mock test series for CTET & State TET Exam by signing up for free. Attempt गणित पत्र 2 (अनुपात और समानुपात) | 10 questions in 10 minutes | Mock test for CTET & State TET preparation | Free important questions MCQ to study for CTET & State TET Exam | Download free PDF with solutions
गणित पत्र 2 (अनुपात और समानुपात) - Question 1
Save

A, B और C की वेतन का अनुपात 5 : 11 : 6 है। यदि उनका कुल वेतन ₹2750 है, तो C द्वारा प्राप्त वेतन का पता लगाएं?(₹ में)

Detailed Solution for गणित पत्र 2 (अनुपात और समानुपात) - Question 1

दिया गया:

A : B : C = 5 : 11 : 6

कुल वेतन = ₹2750

गणना:

C द्वारा प्राप्त वेतन = (6/(5+11+6)) × 2750 = ₹750

∴ C द्वारा प्राप्त वेतन ₹750 है।

गणित पत्र 2 (अनुपात और समानुपात) - Question 2
Save

तीन संख्याओं का योग 370 है। पहली संख्या तीसरी संख्या का 1/4 है, और दूसरी संख्या और तीसरी संख्या का अनुपात 3 : 5 है। तीसरी संख्या ज्ञात कीजिए।

Detailed Solution for गणित पत्र 2 (अनुपात और समानुपात) - Question 2

दी गई:

तीन संख्याओं का योग = 370

पहली संख्या = तीसरी संख्या का 1/4 भाग

दूसरी संख्या और तीसरी संख्या का अनुपात = 3 : 5

गणना:

प्रश्न के अनुसार

मान लेते हैं, दूसरी संख्या = 3X और तीसरी संख्या = 5X

और, पहली संख्या = (1/4) × 5X = 5X/4

अब, (5X/4) + 3X + 5X = 370

⇒ (5X/4) + 8X = 370

⇒ 37X/4 = 370

⇒ X = (370 × 4)/37 = 40

तीसरी संख्या = 5 × 40 = 200

∴ सही उत्तर 200 है

Clear all your doubts with EduRev
गणित पत्र 2 (अनुपात और समानुपात) - Question 3
Save

यदि A ∶ B ∶ C = 2 ∶ 3 ∶ 4 है, तो A ∶ B ∶ C बराबर है -

Detailed Solution for गणित पत्र 2 (अनुपात और समानुपात) - Question 3

दी गई जानकारी:

A ∶ B ∶ C = 2 ∶ 3 ∶ 4

गणना:

मान लें A = 2x, B = 3x और C = 4x

दिए गए समीकरण का मान ज्ञात करें   ∶  ∶  ,

का मान है 

⇒  = (2x/3x)

⇒  = (2/3)

का मान 

⇒  = (3x/4x)

⇒  = (3/4)

का मान 

⇒  = (4x/2x)

⇒  = (2/1)

 ⇒  ∶ 
गणित पत्र 2 (अनुपात और समानुपात) - Question 4
Save

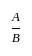
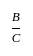
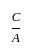
एक डिब्बे में ₹10 के नोट, ₹20 के नोट और ₹50 के नोटों का अनुपात 3 ∶ 5 ∶ 7 है। नोटों की कुल राशि ₹3,360 है। ₹20 और ₹50 के नोटों की संख्या मिलाकर ज्ञात करें।
Detailed Solution for गणित पत्र 2 (अनुपात और समानुपात) - Question 4

दी गई जानकारी:

₹10 के नोट, ₹20 के नोट और ₹50 के नोटों का अनुपात 3N ∶ 5N ∶ 7N है।

नोटों की कुल राशि ₹3,360 है।

गणना:

प्रश्न के अनुसार,

(10 × 3N) + (20 × 5N) + (50 × 7N) = 3360

⇒ 30N + 100N + 350N = 3360

⇒ 480N = 3360

⇒ N = 3360/480

⇒ N = 7

अब,

₹20 के नोटों की संख्या = 5 × 7 = 35

₹50 के नोटों की संख्या = 7 × 7 = 49

₹20 और ₹50 के नोट मिलाकर:

⇒ 35 + 49 = 84

∴ ₹20 और ₹50 के नोटों की संख्या मिलाकर 84 है।

गणित पत्र 2 (अनुपात और समानुपात) - Question 5
Save

यदि = और = , तो है :
Detailed Solution for गणित पत्र 2 (अनुपात और समानुपात) - Question 5

दिया गया:

a/b = 7/11

b/c = 12/17

उपयोग किया गया सिद्धांत:

यदि अनुपात a : b1 और b2 : c में b1 = b2 = b है

तो, अनुपात को a : b : c के रूप में लिखा जा सकता है

गणना:

हमारे पास दोनों भिन्नों में b सामान्य है

b को समान करने के लिए a/b को 12 से और b/c को 11 से गुणा करें

a/b = (7/11) × 12 = 84/132

b/c = (12/17) × 11 = 132/187

इसलिए, a : b : c = 84 : 132 : 187

अब, a + b = 84 + 132 = 216 इकाइयाँ

और, b + c = 132 + 187 = 319 इकाइयाँ

⇒ (a + b)/(b + c) = 216/319

अतः, (a + b)/(b + c) का मान 216/319 है।

गणित पत्र 2 (अनुपात और समानुपात) - Question 6
Save

रवि, रमेश और सुरेश मिलकर ₹1,680 में काम कर सकते हैं। यदि रवि और रमेश मिलकर काम का एक हिस्सा करने वाले हैं, तो सुरेश का हिस्सा (₹ में) होना चाहिए:
Detailed Solution for गणित पत्र 2 (अनुपात और समानुपात) - Question 6

दी गई:

रवि, रमेश और सुरेश मिलकर ₹1,680 के लिए काम कर सकते हैं।

रवि और रमेश मिलकर काम का 9/16 हिस्सा करेंगे।

उपयोग किया गया सूत्र:

भुगतान की गई राशि काम के प्रतिशत के सीधे अनुपात में होती है।

कुशलता = 1/समय।

समाधान:

उपरोक्त सूत्र के अनुसार:

रवि और रमेश को मिलाकर दी गई राशि = 9/16 × 1680 = 945

सुरेश को दी गई राशि = 1680 - 945 = 735

∴ सुरेश का हिस्सा 735 है।

गणित पत्र 2 (अनुपात और समानुपात) - Question 7
Save

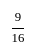
यदि छात्रों की कुल संख्या 2400 है और लड़कों और लड़कियों का अनुपात 7:5 है, तो लड़कियों की संख्या कितनी होगी?
Detailed Solution for गणित पत्र 2 (अनुपात और समानुपात) - Question 7

दिया गया:

कुल छात्र = 2400

लड़कों और लड़कियों का अनुपात = 7: 5

उपयोग किया गया सिद्धांत:

कुल अनुपात इकाइयाँ = अनुपात भागों का योग

लड़कियों की संख्या = (कुल छात्र × लड़कियों की अनुपात इकाइयाँ) / कुल अनुपात इकाइयाँ

गणना:

कुल अनुपात इकाइयाँ = 7 + 5 = 12

⇒ लड़कियों की संख्या = (2400 × 5) / 12

⇒ लड़कियों की संख्या = 12000 / 12

⇒ लड़कियों की संख्या = 1000

∴ लड़कियों की संख्या 1000 है।

वैकल्पिक विधि

उपयोग किया गया सिद्धांत:

अनुपात के अनुपात का सिद्धांत का उपयोग करें।

गणना:

लड़कियों (G) के लिए अनुपात समीकरण सेट करें जो दिए गए अनुपात पर आधारित है:

लड़के (B) : लड़कियाँ (G) = 7 : 5

एक चर के संदर्भ में अनुपात को व्यक्त करें (मान लें कि x सामान्य गुणांक है):

B = 7x & G = 5x

अनुपातों का योग कुल छात्रों की संख्या के बराबर है:

7x + 5x = 2400

समान तत्वों को मिलाएँ:

12x = 2400

⇒ x = 200

लड़कियों की संख्या (G) ज्ञात करें:

G = 5 × 200

⇒ G = 1000

∴ लड़कियों की संख्या 1000 है।

गणित पत्र 2 (अनुपात और समानुपात) - Question 8
Save

x y के वर्ग के अनुसार सीधा और z के घनमूल के अनुसार उलटा बदलता है और x = 2 है, जब y = 4, z = 8। जब x = 3 और z = 27, तब y का मान क्या है?
Detailed Solution for गणित पत्र 2 (अनुपात और समानुपात) - Question 8

दी गई जानकारी:

सीधा परिवर्तन संबंध = x ∝ y2।

उलटा परिवर्तन संबंध = x ∝ 1/z(1/3)।

उपयोग की गई अवधारणा:

परिवर्तन समस्याओं में, अनुपात के स्थिरांक को स्थापित करना समानता में परिवर्तन की अनुमति देता है।

गणनाएँ:

x = k (y2/z(1/3)) जहाँ k अनुपात का स्थिरांक है।

x = 2, y = 4, और z = 8 को प्रतिस्थापित करते हुए

⇒ 2 = k((42) ÷ (8(1/3)))

⇒ k = 0.25

अब x = 3, z = 27, और k = 0.25 को प्रतिस्थापित करते हुए

⇒ 3 = 0.25(y2/(27(1/3))).

⇒ 3 = 0.25(y2/3)

⇒ y2 = 900/25

⇒ y2 = ±36.

⇒ y = ±6.

∴ y या तो 6 या -6 हो सकता है।

गणित पत्र 2 (अनुपात और समानुपात) - Question 9
Save

दो संख्याएँ क्रमशः 4 : 5 के अनुपात में हैं। यदि प्रत्येक संख्या को 25 घटाया जाए, तो अनुपात 3 : 4 हो जाता है।largest number ज्ञात करें।
Detailed Solution for गणित पत्र 2 (अनुपात और समानुपात) - Question 9

दिया गया:

दो संख्याओं का मूल अनुपात = 4 : 5

दो संख्याओं का परिवर्तित अनुपात = 3 : 4

प्रत्येक संख्या को 25 घटाने पर

गणना:

मान लीजिए कि मूल संख्याएँ 4x और 5x हैं।

प्रश्न के अनुसार,

16x - 100 = 15x - 75

⇒ 16x - 15x = 100 - 75

⇒ x = 25

बड़ी संख्या = 5x = 5 × 25 = 125

∴ सबसे बड़ी संख्या 125 है।

गणित पत्र 2 (अनुपात और समानुपात) - Question 10
Save

एक आइस-क्रीम फैक्ट्री में 840 श्रमिकों में पुरुषों और महिलाओं का अनुपात 5 : 7 है। अनुपात 1 : 1 बनाने के लिए और कितने पुरुषों को जोड़ा जाना चाहिए?
Detailed Solution for गणित पत्र 2 (अनुपात और समानुपात) - Question 10

शॉर्टकट ट्रिक

पुरुष : महिलाएँ = 5 : 7

कर्मचारियों की कुल संख्या = 840

⇒ 12 का मान → 840

⇒ 1 का मान → 70

चूंकि अधिक पुरुष जुड़ रहे हैं। लेकिन महिलाएँ वही हैं।

⇒ 2 का मान → 70 × 2 = 140

इसलिए, अनुपात 1 : 1 बनाने के लिए 140 और पुरुषों को जोड़ा जाना चाहिए।

वैकल्पिक विधि

मान लीजिए कि आइसक्रीम फैक्ट्री में पुरुष और महिलाएँ क्रमशः 5x और 7x हैं।

⇒ 5x + 7x = 840

⇒ 12x = 840

⇒ x = 70

इसलिए, पुरुष = 5x = 5 × 70 = 350

और महिलाएँ = 7x = 7 × 70 = 490

मान लीजिए कि y और पुरुषों को जोड़ा जाना चाहिए ताकि अनुपात 1 : 1 हो।

⇒ 350 + y = 490

⇒ y = 140

इसलिए, अनुपात 1 : 1 बनाने के लिए 140 और पुरुषों को जोड़ा जाना चाहिए।

Information about गणित पत्र 2 (अनुपात और समानुपात) Page
In this test you can find the Exam questions for गणित पत्र 2 (अनुपात और समानुपात) solved & explained in the simplest way possible. Besides giving Questions and answers for गणित पत्र 2 (अनुपात और समानुपात), EduRev gives you an ample number of Online tests for practice
Download as PDF

Important Questions for गणित पत्र 2 (अनुपात और समानुपात)

Find all the important questions for गणित पत्र 2 (अनुपात और समानुपात) at EduRev.Get fully prepared for गणित पत्र 2 (अनुपात और समानुपात) with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the गणित पत्र 2 (अनुपात और समानुपात) syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of गणित पत्र 2 (अनुपात और समानुपात) resources.

गणित पत्र 2 (अनुपात और समानुपात) MCQs with Answers

Prepare for the गणित पत्र 2 (अनुपात और समानुपात) within the CTET & State TET exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for गणित पत्र 2 (अनुपात और समानुपात)

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace गणित पत्र 2 (अनुपात और समानुपात) with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up
within 7 days!
Takes less than 10 seconds to signup