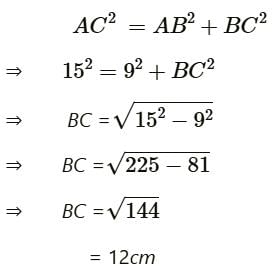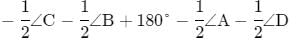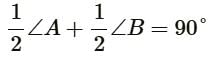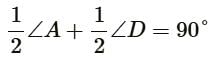परीक्षा: चतुर्भुज - 2 - CTET & State TET MCQ
25 Questions MCQ Test - परीक्षा: चतुर्भुज - 2
दो पैरालेलोग्राम समान आधार पर खड़े हैं और समान समानांतर रेखाओं के बीच हैं। उनके क्षेत्रफल का अनुपात क्या है?
चतुर्भुज ABCD में, यदि ∠A = 60∘ और ∠B : ∠C : ∠D = 2:3:7, तो ∠D कितना है:
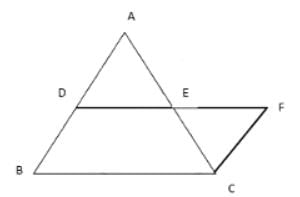
D और E त्रिकोण ABC के भुजाओं AB और AC के मध्य बिंदु हैं। DE को F तक बढ़ाया गया है। यह प्रमाणित करने के लिए कि CF DA के समान और समानांतर है, हमें एक अतिरिक्त जानकारी की आवश्यकता है जो है:
P, Q, R त्रिभुज ABC के किनारों AB, BC और AC के मध्य बिंदु हैं। यदि AB = 10 सेमी, BC = 8 सेमी, AC = 12 सेमी है, तो ΔPQR का परिमाप ज्ञात करें।
त्रिकोण ABC जिसमें B पर समकोण है। दिया गया है कि AB = 9 सेमी, AC = 15 सेमी और D, E क्रमशः AB और AC के मध्य बिंदु हैं। BC की लंबाई ज्ञात कीजिये।
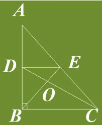
नीचे तीन कथन दिए गए हैं:
(I) एक समांतर चतुर्भुज में, 2 आसन्न कोणों के कोण बिसेक्टर एक समकोण बनाते हैं।
(II) समांतर चतुर्भुज के कोण बिसेक्टर एक आयत बनाते हैं।
(III) एक समद्विबाहु त्रिकोण के भुजाओं के मध्य बिंदुओं को जोड़ने से बना त्रिकोण आवश्यक रूप से समद्विबाहु त्रिकोण नहीं होता। कौन सा सत्य है?
यदि APB और CQD 2 समांतर रेखाएँ हैं, तो कोण APQ, BPQ, CQP और PQD के बिसेक्टर केवल तब एक वर्ग बनाएंगे जब
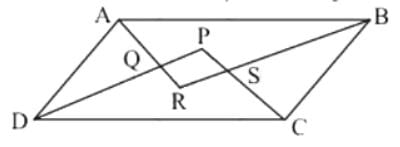
यदि चतुष्कोण ABCD के कोण A और कोण B की बाइसेक्टर एक-दूसरे को P पर, कोण B और कोण C पर Q पर, कोण C और कोण D पर R पर, और कोण D और कोण A पर S पर मिलती हैं, तो PQRS एक है
समलंबी चतुर्भुज ABCD के विकर्ण AC और BD एक दूसरे को बिंदु O पर इस प्रकार काटते हैं कि ∠DAC = 30∘ और ∠AOB = 70∘। तब, ∠DBC क्या होगा?
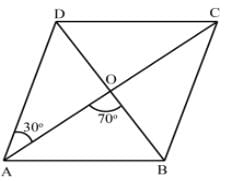
समांतर चतुर्भुज ABCD में, कोण A और B की बिसेक्टर एक-दूसरे को O पर काटती हैं। AOB का माप ∠ है।
नीचे तीन कथन दिए गए हैं:
(I) आयत ABCD में, तिर्यक AC कोण A और कोण C को आधा करता है।
(II) वर्ग ABCD में, तिर्यक AC कोण A और कोण C को आधा करता है।
(III) समांतर भुजाओं का ABCD में, तिर्यक AC कोण A और कोण C को आधा करता है।
कौन सा सत्य है?
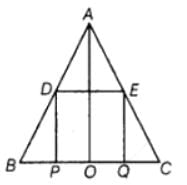
डी और ई त्रिभुज ABC के पक्ष AB और AC के मध्य बिंदु हैं और O BC के पक्ष पर कोई भी बिंदु है, O को A से जोड़ा गया है। यदि P और Q OB और OC के मध्य बिंदु हैं, तो DEQP क्या है?
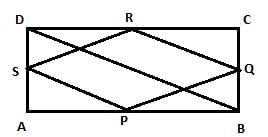
दी गई आयत ABCD में P, Q, R और S क्रमशः AB, BC, CD और DA के मध्य बिंदु हैं। यदि आयत के एक विकर्ण की लंबाई 8 सेमी है, तो चतुर्भुज PQRS एक है।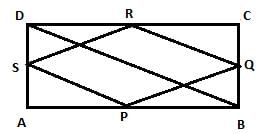
DE और E, त्रिकोण ABC के पक्ष AB और AC के मध्य बिंदु हैं। यदि BC = 5.6cm है, तो DE ज्ञात करें।
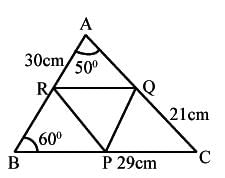
एक त्रिकोण में P, Q और R क्रमशः BC, CA और AB के मध्य बिंदु हैं। यदि AC = 21 सेमी, BC = 29 सेमी और AB = 30 सेमी है, तो चतुर्भुज ARPQ का परिमाण ज्ञात करें?
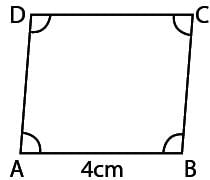
चतुर्भुज ABCD के विपरीत कोण समान हैं। यदि AB = 4 सेमी है, तो CD की लंबाई ज्ञात कीजिए।
चतुर्भुज ABCD में, ∠B = 90∘, ∠C−∠D = 60∘ और ∠A−∠C−∠D = 10∘ है। ∠A, ∠C और ∠D का मान ज्ञात करें।
यदि एक चतुर्भुज ABCD है, जहां ∠A = 90∘ और AB = BC = CD = DA है, तो ABCD कौन सा होगा?
त्रिकोण △ABC में, EF वह रेखा खंड है जो AB और AC की भुजाओं के मध्य बिंदुओं को जोड़ता है। BC = 7.2 सेमी है, EF ज्ञात करें।
चित्र में, ABCD एक समचतुर्भुज है, जिसके विकर्ण 0 पर मिलते हैं। x और y के मान ज्ञात करें।
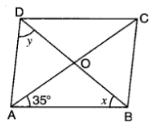
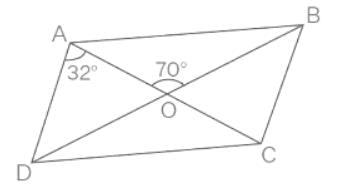
पैराललोग्राम ABCD के विकर्ण AC और BD एक दूसरे को बिंदु O पर इंटरसेक्ट करते हैं। यदि ∠DAC = 32∘ और ∠AOB = 70∘ है, तो ∠DBC के बराबर क्या है?