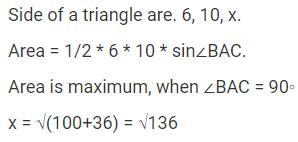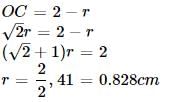परीक्षा: ज्यामिति - 2 - CTET & State TET MCQ
15 Questions MCQ Test - परीक्षा: ज्यामिति - 2
एक चक्रीय चतुर्भुज ऐसा होता है कि इसके दो आसन्न कोण क्रमशः 6 और 10 से विभाजित होते हैं। शेष कोणों में से एक को अनिवार्य रूप से विभाजित किया जाएगा:
दो गेंदों के आयतन का अनुपात 27 : 125 है। उनके सतह क्षेत्र का अनुपात क्या होगा?
एक त्रिकोण की भुजाएँ 6, 10 और x हैं, x के लिए वह मान क्या है जिससे त्रिकोण का क्षेत्रफल अधिकतम होगा?
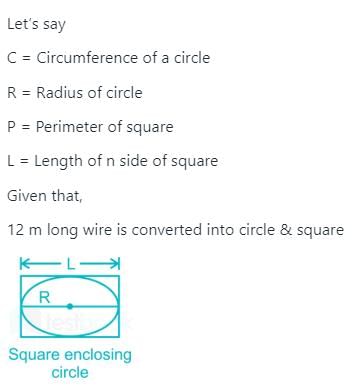
एक वर्ग को 10 सेमी त्रिज्या के अर्धवृत्त में अंकित किया गया है। अंकित वर्ग का क्षेत्रफल क्या है? (यह दिया गया है कि वर्ग का एक भुजा अर्धवृत्त के व्यास के साथ है।)
दिए गए अर्धवृत्त में बिना किसी ओवरलैप के समान त्रिज्या वाले दो वृत्त बनाए गए हैं। यदि ये अर्धवृत्त द्वारा समाहित किए जा सकने वाले सबसे बड़े वृत्त हैं, तो प्रत्येक वृत्त की त्रिज्या (सेमी में) क्या होगी?
PQRS एक ट्रैपेजियम है, जिसमें PQ RS के समानांतर है, और PQ = 3 (RS) है। ट्रैपेजियम की विकर्ण X पर एक-दूसरे को काटते हैं, तब, अनुपात, ar ( ∆ PXQ) : ar ( ∆ RXS) क्या होगा?
मान लीजिए कि ABCDEF एक नियमित षट्कोण है। त्रिकोण ACE के क्षेत्रफल का अनुपात षट्कोण ABCDEF के क्षेत्रफल के साथ क्या है?
एक तालाब जिसका व्यास 100 मीटर है, एक गोलाकार घास के रास्ते द्वारा घिरा हुआ है जो 2 मीटर चौड़ा है। घास के रास्ते पर कितने वर्ग मीटर घास है?
एक आयताकार बॉक्स के आयामों का अनुपात 1:2:4 है और इसे कपड़े और चादर से ढकने की लागत के बीच का अंतर क्रमशः 20 रुपये और 20.5 रुपये प्रति वर्ग मीटर है, जो कि 126 रुपये है। बॉक्स के आयाम ज्ञात कीजिए।
एक अर्धवृत्त में अंकित वर्ग के क्षेत्रफल का अनुपात उसी त्रिज्या वाले वृत्त में अंकित वर्ग के क्षेत्रफल के साथ क्या है?
एक वर्ग के क्षेत्रफल का अनुपात उस वर्ग के क्षेत्रफल के साथ क्या होता है जो इसके विकर्ण पर खींचा गया है?
उन त्रिकोण का क्षेत्रफल क्या है जिसमें दो मीडियन 9 सेमी और 12 सेमी लंबे हैं और जो एक दूसरे पर समकोण पर मिलते हैं?
चार घोड़े एक 14 मीटर लंबी भुजा वाले वर्गीय भूखंड के चार कोनों पर बंधे हैं, ताकि निकटवर्ती घोड़े एक-दूसरे तक पहुँच सकें। केंद्र में 20 मीटर² क्षेत्रफल का एक छोटा गोलाकार तालाब है। अघासित क्षेत्रफल ज्ञात करें।
एक त्रिकोण की दो भुजाएँ 4 और 5 हैं। तब, त्रिकोण के क्षेत्रफल के लिए निम्नलिखित में से कौन सी सीमा सबसे सटीक है?