Explore Exams
Login Signup
Sign in Open App
CTET & State TET Exam  >  CTET & State TET Tests  >  परीक्षा: ज्यामिति - 3 - CTET & State TET MCQ

परीक्षा: ज्यामिति - 3 - CTET & State TET MCQ


Test Description

15 Questions MCQ Test - परीक्षा: ज्यामिति - 3

परीक्षा: ज्यामिति - 3 for CTET & State TET 2025 is part of CTET & State TET preparation. The परीक्षा: ज्यामिति - 3 questions and answers have been prepared according to the CTET & State TET exam syllabus.The परीक्षा: ज्यामिति - 3 MCQs are made for CTET & State TET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for परीक्षा: ज्यामिति - 3 below.
Solutions of परीक्षा: ज्यामिति - 3 questions in English are available as part of our course for CTET & State TET & परीक्षा: ज्यामिति - 3 solutions in Hindi for CTET & State TET course. Download more important topics, notes, lectures and mock test series for CTET & State TET Exam by signing up for free. Attempt परीक्षा: ज्यामिति - 3 | 15 questions in 15 minutes | Mock test for CTET & State TET preparation | Free important questions MCQ to study for CTET & State TET Exam | Download free PDF with solutions
परीक्षा: ज्यामिति - 3 - Question 1
Save

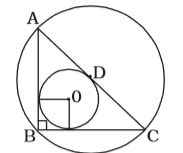
रेखा AB की लंबाई 6 मीटर है और यह दो समवृत्त वृत्तों में से आंतरिक वृत्त के बिंदु C पर स्पर्श करती है। यह ज्ञात है कि दोनों वृत्तों की त्रिज्याएँ पूर्णांक हैं। बाहरी वृत्त की त्रिज्या------- है, जहाँ A और B बाहरी वृत्त पर बिंदु हैं।

Detailed Solution for परीक्षा: ज्यामिति - 3 - Question 1

मान लें कि आंतरिक वृत्त की त्रिज्या r1 है और बाहरी वृत्त की त्रिज्या r2 है। बाहरी वृत्त के एक बिंदु से आंतरिक वृत्त तक स्पर्श रेखा की लंबाई निम्नलिखित दी गई है:
AC2 = AB2 - (r2 - r1)2
दी गई जानकारी के अनुसार AB = 6 मीटर है, और रेखा AB बिंदु C पर आंतरिक वृत्त को स्पर्श करती है, पाइथागोरस प्रमेय के अनुसार:
r22 = r12 + 32
चूंकि त्रिज्याएँ पूर्णांक हैं, इसे हल करने पर हमें r1 = 3 मीटर और r2 = 5 मीटर मिलते हैं। इसलिए, बाहरी वृत्त की त्रिज्या 5 मीटर है।

परीक्षा: ज्यामिति - 3 - Question 2
Save

एक वृत्त की दो रज्जुओं की लंबाई a और b है, जो क्रमशः केंद्र पर 60° और 90° के कोण बनाती हैं। निम्नलिखित में से कौन सा सही है?

Detailed Solution for परीक्षा: ज्यामिति - 3 - Question 2

इस समस्या का समाधान करने के लिए, हम रज्जु (chord) और केंद्र (center) के बीच के संबंध को समझते हैं। रज्जु की लंबाई और केंद्र पर बनाए गए कोण के बीच एक निश्चित संबंध होता है। यहाँ 60° और 90° के कोनों को देखते हुए, हम गणना कर सकते हैं कि b = √2a सही उत्तर है।

Clear all your doubts with EduRev
परीक्षा: ज्यामिति - 3 - Question 3
Save

32 सेमी लंबाई का एक कर्ड एक वृत्त के अंदर रखा गया है जिसका त्रिज्या 20 सेमी है और एक बिंदु जो वृत्त के केंद्र से 13 सेमी की दूरी पर है, कर्ड पर चिह्नित किया गया है। कर्ड के खंडों की लंबाई की गणना करें।

Detailed Solution for परीक्षा: ज्यामिति - 3 - Question 3

AQ = (16 + 5 = 21) सेमी और QB = 32 - 21 = 11 सेमी

परीक्षा: ज्यामिति - 3 - Question 4
Save

एक समकोण त्रिकोण X से सबसे बड़ा संभव नियमित षट्कोण H काटा गया है। षट्कोण H से सबसे बड़ा संभव समकोण त्रिकोण Y काटा गया है। समकोण त्रिकोण X और Y के क्षेत्रों का अनुपात क्या है?
Detailed Solution for परीक्षा: ज्यामिति - 3 - Question 4

परीक्षा: ज्यामिति - 3 - Question 5
Save

किसी भी चतुर्भुज ABCD में, विकर्ण AC और BD एक बिंदु X पर मिलते हैं। यदि E, F, G और H क्रमशः AX, BX, CX और DX के मध्य बिंदु हैं, तो (EF + FG + GH + GE) का अनुपात (AD + DC + CB + BA) के साथ क्या है?
Detailed Solution for परीक्षा: ज्यामिति - 3 - Question 5

एक मध्य बिंदु एक रेखा खंड पर एक बिंदु है जो दोनों अंतिम बिंदुओं से समान दूरी पर होता है। मध्य बिंदु प्रमेय यह बताने के लिए उपयोग किया जाता है कि त्रिकोण के भुजाओं और उनके लंबाई के बारे में एक मजबूत बयान है। यदि हम एक त्रिकोण लेते हैं, और उसके दो भुजाओं को एक रेखा खंड से जोड़ते हैं, और यह रेखा खंड प्रत्येक भुजा के केंद्रों, या मध्य बिंदुओं पर जुड़ता है, तो हम त्रिकोण के बारे में और भुजाओं के बीच के संबंधों के बारे में दो बहुत महत्वपूर्ण पहलुओं को जान सकते हैं।

परीक्षा: ज्यामिति - 3 - Question 6
Save

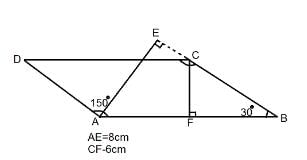
एक पैरालेलोग्राम का एक कोण 150° है। इस कोण के शीर्ष से ऊँचाइयाँ खींची गई हैं। यदि ये ऊँचाइयाँ 6 सेमी और 8 सेमी मापती हैं, तो पैरालेलोग्राम का परिमाप ज्ञात करें।
Detailed Solution for परीक्षा: ज्यामिति - 3 - Question 6

पैरालेलोग्राम का परिमाप ज्ञात करने के लिए, हमें पहले इसके आधार और ऊँचाई के गुणनफल का उपयोग करना होगा। यहाँ, ऊँचाइयाँ 6 सेमी और 8 सेमी हैं। इसके बाद, हम दो उर्ध्वाधर रेखाएँ बनाएँगे, जिनसे हमें परिमाप का पता चलेगा। कुल मिलाकर, पैरालेलोग्राम का परिमाप 56 सेमी है।

परीक्षा: ज्यामिति - 3 - Question 7
Save

चलिए मानते हैं कि C1 और C2 एक त्रिकोण के अंतर्गत और परिधीय वृत्त हैं, जिसकी भुजाएँ 3 सेमी, 4 सेमी और 5 सेमी हैं।
Detailed Solution for परीक्षा: ज्यामिति - 3 - Question 7


परीक्षा: ज्यामिति - 3 - Question 8
Save

PQRS एक त्रैपेजियम है जिसमें PQ और RS समांतर हैं। PQ = 6 सेमी, QR = 5 सेमी, RS = 3 सेमी, PS = 4 सेमी। PQRS का क्षेत्रफल है
Detailed Solution for परीक्षा: ज्यामिति - 3 - Question 8

परीक्षा: ज्यामिति - 3 - Question 9
Save

चित्र से x और y का मान ज्ञात कीजिए। y का मान ज्ञात कीजिए।
Detailed Solution for परीक्षा: ज्यामिति - 3 - Question 9

परीक्षा: ज्यामिति - 3 - Question 10
Save

एक गेंद जिसका व्यास 15 सेमी है, इस प्रकार तैर रही है कि गेंद का शीर्ष तालाब की चिकनी सतह (पानी) से 5 सेमी ऊपर है। पानी की सतह के साथ गेंद के संपर्क द्वारा निर्मित वृत्त का परिमाप सेंटीमीटर में क्या होगा?
Detailed Solution for परीक्षा: ज्यामिति - 3 - Question 10

परीक्षा: ज्यामिति - 3 - Question 11
Save

दो वृत्त APQC और PBDQ एक-दूसरे को P और Q बिंदुओं पर काटते हैं और APB और CQD दो समांतर सीधी रेखाएँ हैं। तब निम्नलिखित में से केवल एक कथन हमेशा सत्य है। वह कौन सा है?
Detailed Solution for परीक्षा: ज्यामिति - 3 - Question 11

ABDC एक चक्रीय चतुर्भुज है, क्योंकि दो वृत्त के चौराहे पर स्थित बिंदु P और Q के प्रति अन्य बिंदुओं से विभाजित रेखाएँ हमेशा एक चक्रीय आकृति बनाती हैं।

परीक्षा: ज्यामिति - 3 - Question 12
Save

तीन घोड़े एक अर्ध-वृत्ताकार मैदान में घास चर रहे हैं। नीचे दिए गए चित्र में, AB अर्ध-वृत्ताकार मैदान का व्यास है जिसका केंद्र O है। घोड़े P, R और S पर बंधे हैं, इस प्रकार कि PO और RO अर्ध-वृत्तों के त्रिज्याएँ हैं जिनके केंद्र P और R हैं, और S वह केंद्र है जो AO और OB के व्यास के साथ दो अर्ध-वृत्तों को स्पर्श करता है। P और R पर बंधे घोड़े अपने-अपने अर्ध-वृत्त में घास चर सकते हैं, जबकि S पर बंधा घोड़ा S के केंद्र वाले वृत्त में घास चर सकता है। AB व्यास वाले अर्ध-वृत्तों के क्षेत्रफल का प्रतिशत जो घोड़ों द्वारा नहीं चराया जा सकता, उसके निकटतम मान है
Detailed Solution for परीक्षा: ज्यामिति - 3 - Question 12

परीक्षा: ज्यामिति - 3 - Question 13
Save

निम्नलिखित आकृति पर विचार करें: AB = 10 सेमी, AC = 17 सेमी, BC = 21 सेमी और EHFD एक वर्ग है। वर्ग की भुजाओं की लंबाई ज्ञात कीजिए (सेमी में)।
Detailed Solution for परीक्षा: ज्यामिति - 3 - Question 13

वर्ग की भुजा हमेशा त्रिकोण की ऊँचाई से कम होनी चाहिए।

परीक्षा: ज्यामिति - 3 - Question 14
Save

एक नियमित अष्टकोण जो 1 सेमी की त्रिज्या के वृत्त में अंकित है, उसके एक निश्चित शीर्ष से अन्य सात शीर्षों तक की दूरी का गुणनफल क्या है?
Detailed Solution for परीक्षा: ज्यामिति - 3 - Question 14

हमें AH x AG x AF x AE x AD x AC x AB का गुणनफल निकालना है।

AE = 2

 कोसाइन सूत्र का उपयोग करके A G (= A C) और A F (= AD) प्राप्त करें।

परीक्षा: ज्यामिति - 3 - Question 15
Save

10 सेमी व्यास की एक अंगूठी को केंद्र के ठीक ऊपर 12 सेमी की ऊँचाई पर एक बिंदु से छह समान तारों के द्वारा लटकाया गया है। ये तारे अंगूठी की परिधि पर समान अंतराल पर जुड़े हुए हैं, जिससे अंगूठी एक क्षैतिज तल में बनी रहती है। दो निकटतम तारों के बीच के कोण का कोसाइन मान निम्नलिखित के बीच है।
Detailed Solution for परीक्षा: ज्यामिति - 3 - Question 15

समस्या को एक सामान्य षट्कोण के आधार पर एक पिरामिड के रूप में विचार करें।
अब A POR में

OP = 12 सेमी

OR = 5 सेमी

PR = 13 सेमी

अब कोसाइन सूत्र उत्तर देगा।

Information about परीक्षा: ज्यामिति - 3 Page
In this test you can find the Exam questions for परीक्षा: ज्यामिति - 3 solved & explained in the simplest way possible. Besides giving Questions and answers for परीक्षा: ज्यामिति - 3, EduRev gives you an ample number of Online tests for practice
Download as PDF

Important Questions for परीक्षा: ज्यामिति - 3

Find all the important questions for परीक्षा: ज्यामिति - 3 at EduRev.Get fully prepared for परीक्षा: ज्यामिति - 3 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the परीक्षा: ज्यामिति - 3 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of परीक्षा: ज्यामिति - 3 resources.

परीक्षा: ज्यामिति - 3 MCQs with Answers

Prepare for the परीक्षा: ज्यामिति - 3 within the CTET & State TET exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for परीक्षा: ज्यामिति - 3

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace परीक्षा: ज्यामिति - 3 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up
within 7 days!
Takes less than 10 seconds to signup