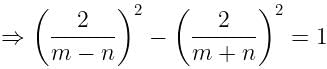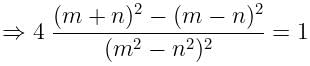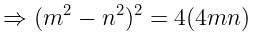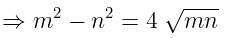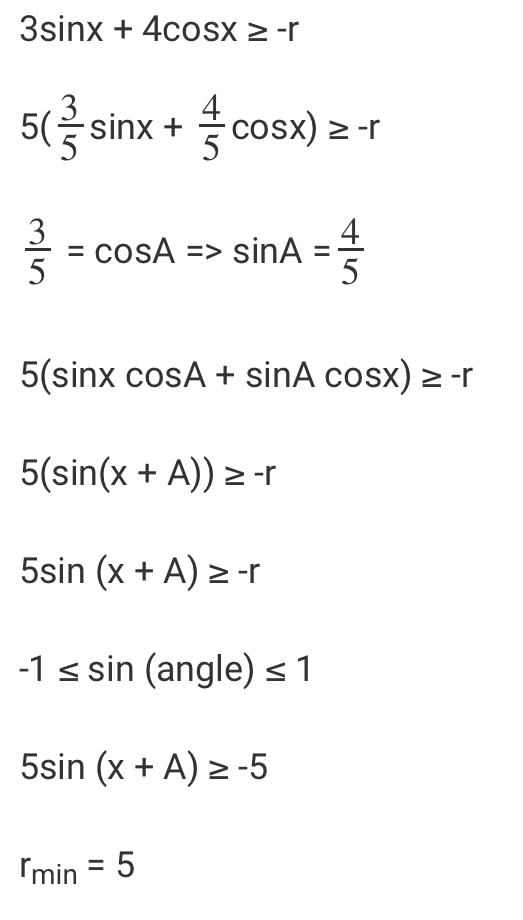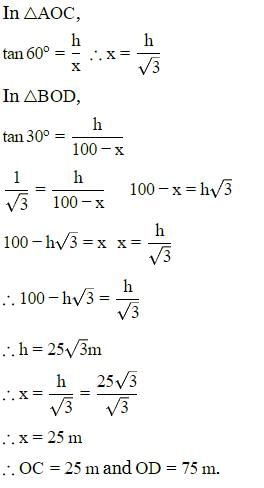परीक्षा: त्रिकोणमिति - 1 - Bank Exams MCQ
10 Questions MCQ Test Quantitative Aptitude/संख्यात्मक योग्यता - परीक्षा: त्रिकोणमिति - 1
एक छात्र 100 मीटर ऊंची कॉलेज बिल्डिंग की छत पर एक बैनर के साथ खड़ा है। ज़मीन पर एक बिंदु से, छात्र के शीर्ष का ऊंचाई कोण 60° है और उसी बिंदु से, टॉवर के शीर्ष का ऊंचाई कोण 45° है। छात्र की ऊँचाई ज्ञात करें।
यदि sin (A + B) = √3 / 2 और tan (A – B) = 1 है, तो A और B के मान क्या हैं?
यदि tanØ + sinØ = m, tanØ - sinØ = n, तो m2 - n2. का मान ज्ञात करें।
यदि cos A + cos2 A = 1 और a sin12 A + b sin10 A + c sin8 A + d sin6 A - 1 = 0 हो। तो a+b / c+d का मान ज्ञात करें।
3sinx + 4cosx + r हमेशा 0 से बड़ा या उसके बराबर है। 'r' का सबसे छोटा मान क्या हो सकता है?
एक समकोण त्रिकोण की ऊँचाई 'p', आधार 'b' और कर्ण 'h' है। निम्नलिखित में से कौन सा मान h2 नहीं ले सकता है, यह मानते हुए कि p और b सकारात्मक पूर्णांक हैं?
यदि कोस x - साइन x = √2 साइन x है, तो कोस x + साइन x का मान ज्ञात कीजिए:
दो समान ऊँचाई वाले पोल एक सड़क के दोनों ओर आमने-सामने खड़े हैं, जो 100 मीटर चौड़ी है। उनके बीच सड़क पर एक बिंदु खोजें, जहाँ उनके शीर्षों के लिए ऊँचाई के कोण क्रमशः 30° और 60° हैं। प्रत्येक पोल की ऊँचाई (मीटर में) क्या है?
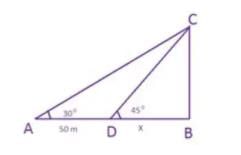
अनिल ने अपनी नाव से एक लाइटहाउस के शीर्ष की ओर देखा और पाया कि ऊँचाई का कोण 30 डिग्री है। लाइटहाउस की ओर 50 मीटर की सीधी रेखा में चलने के बाद, उसने पाया कि ऊँचाई का कोण 45 डिग्री हो गया। लाइटहाउस की ऊँचाई ज्ञात करें।
दो पोलों के शीर्ष, जिनकी ऊँचाई क्रमशः 30 मीटर और 14 मीटर है, एक तार से जुड़े हुए हैं। यदि तार क्षैतिज के साथ 30° का कोण बनाता है, तो तार की लंबाई ज्ञात करें।
|
171 docs|185 tests
|