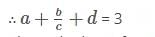All Courses
Get the App Signup / Login
Sign in Open App
Bank Exams Exam  >  Bank Exams Tests  >  Quantitative Aptitude/संख्यात्मक योग्यता  >  परीक्षा: त्रिकोणमिति- 2 - Bank Exams MCQ

परीक्षा: त्रिकोणमिति- 2 - Bank Exams MCQ


Test Description

10 Questions MCQ Test Quantitative Aptitude/संख्यात्मक योग्यता - परीक्षा: त्रिकोणमिति- 2

परीक्षा: त्रिकोणमिति- 2 for Bank Exams 2025 is part of Quantitative Aptitude/संख्यात्मक योग्यता preparation. The परीक्षा: त्रिकोणमिति- 2 questions and answers have been prepared according to the Bank Exams exam syllabus.The परीक्षा: त्रिकोणमिति- 2 MCQs are made for Bank Exams 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for परीक्षा: त्रिकोणमिति- 2 below.
Solutions of परीक्षा: त्रिकोणमिति- 2 questions in English are available as part of our Quantitative Aptitude/संख्यात्मक योग्यता for Bank Exams & परीक्षा: त्रिकोणमिति- 2 solutions in Hindi for Quantitative Aptitude/संख्यात्मक योग्यता course. Download more important topics, notes, lectures and mock test series for Bank Exams Exam by signing up for free. Attempt परीक्षा: त्रिकोणमिति- 2 | 10 questions in 10 minutes | Mock test for Bank Exams preparation | Free important questions MCQ to study Quantitative Aptitude/संख्यात्मक योग्यता for Bank Exams Exam | Download free PDF with solutions
परीक्षा: त्रिकोणमिति- 2 - Question 1
Save

अभ्यास प्रश्न या MCQ (बहुविकल्पीय प्रश्न) हल के साथ उपलब्ध हैं, जो आपको त्रिकोणमिति के लिए तैयारी में मदद करेंगे, जो गुणात्मक योग्यता के अंतर्गत आता है। आप अपनी गति के अनुसार इन अभ्यास प्रश्नों का अभ्यास कर सकते हैं और विषय में सुधार कर सकते हैं। यह विषय विभिन्न प्रतियोगी परीक्षाओं जैसे - CAT, GMAT, बैंक PO, SSC और अन्य प्रतियोगी परीक्षाओं में शामिल किया गया है।

 

प्रश्न. 3sinx + 4cosx + r हमेशा 0 से अधिक या उसके बराबर है। सबसे छोटी मान 'r' क्या हो सकती है?

Detailed Solution for परीक्षा: त्रिकोणमिति- 2 - Question 1

परीक्षा: त्रिकोणमिति- 2 - Question 2
Save

sin2014x + cos2014x = 1, x की सीमा [-5π, 5π] में, x कितने मान ले सकता है?

Detailed Solution for परीक्षा: त्रिकोणमिति- 2 - Question 2

हमें ज्ञात है कि sin2x + cos2x = 1 सभी x के मानों के लिए।
यदि sin x या cos x -1 या 1 के बराबर है, तो sin2014x + cos2014x 1 के बराबर होगा।

sin x -1 या 1 के बराबर तब होता है जब x = -4.5π या -3.5π या -2.5π या -1.5π या -0.5π या 0.5π या 1.5π या 2.5π या 3.5π या 4.5π।
cos x -1 या 1 के बराबर तब होता है जब x = -5π या -4π या -3π या -2π या -π या 0 या π या 2π या 3π या 4π या 5π।

अन्य सभी मानों के लिए, sin2014x sin2x से कम होगा।
अन्य सभी मानों के लिए, cos2014x cos2x से कम होगा।

हमें ज्ञात है कि sin2x + cos2x 1 के बराबर है। इसलिए, sin2014x + cos2014x अन्य सभी मानों के लिए 1 के बराबर नहीं होगा। इस प्रकार, 21 मान हैं।
उत्तर विकल्प (C)

Clear all your doubts with EduRev
परीक्षा: त्रिकोणमिति- 2 - Question 3
Save

एक नियमित षट्भुज ABCDEF पर B और D पर टॉवर लगाए गए हैं। A से टॉवर B तक के लिए लिफ्ट का कोण 30 डिग्री है, और टॉवर D के शीर्ष तक 45 डिग्री है। B और D पर टॉवर की ऊंचाइयों का अनुपात क्या है?

Detailed Solution for परीक्षा: त्रिकोणमिति- 2 - Question 3

मान लीजिए कि षट्भुज ABCDEF की भुजा a है। रेखा AD = 2a है। टॉवर B और D को B’B और D’D मान लें।
दिए गए डेटा से हमें पता है कि ∠B´AB = 30° और ∠D´AB = 45° है। ध्यान रखें कि टॉवर B’B और D´D उसी विमान में नहीं हैं जैसे षट्भुज।

परीक्षा: त्रिकोणमिति- 2 - Question 4
Save

8 cos A + 15 sin A + 15 का अधिकतम और न्यूनतम मान निकालें।
Detailed Solution for परीक्षा: त्रिकोणमिति- 2 - Question 4

इस समीकरण का अधिकतम मान 11√2 + 15 है और न्यूनतम मान 15 है।

परीक्षा: त्रिकोणमिति- 2 - Question 5
Save

यदि cos A + cos2A = 1 और a sin12A + b sin10A + c sin8A + d sin6A - 1 = 0 है। तो का मान ज्ञात करें।
Detailed Solution for परीक्षा: त्रिकोणमिति- 2 - Question 5

दी गई जानकारी:
cos A = 1 - cos2A
=) cos A = sin2A
=) cos2A = sin4A
=) 1 - sin2A = sin4A
=) 1 = sin4A + sin2A
=) 13 = (sin4A + sin2A)3
=) 1 = sin12A + sin6A + 3sin8A + 3sin10A
=) sin12A + sin6A + 3sin8A + 3sin10A - 1 = 0
तुलना करने पर,
a = 1, b = 3, c = 3, d = 1

विकल्प (B) सही है।

परीक्षा: त्रिकोणमिति- 2 - Question 6
Save

उपर्युक्त चित्र में, चौड़ाई W की चादर PQ के साथ इस प्रकार मोड़ी जाती है कि R S पर ओवरलैप हो जाता है। PQ की लंबाई को इस प्रकार लिखा जा सकता है :-
Detailed Solution for परीक्षा: त्रिकोणमिति- 2 - Question 6

यदि आप अवलोकन में तेज हैं, तो यह प्रश्न केवल विकल्पों को देखकर हल किया जा सकता है क्योंकि,

हम चित्र को इस प्रकार खींच सकते हैं :-


उत्तर विकल्प (D)

परीक्षा: त्रिकोणमिति- 2 - Question 7
Save

मान निकालिए :- (लॉग साइन 1° + लॉग साइन 2° + ... + लॉग साइन 89°) + (लॉग टैन 1° + लॉग टैन 2° + ... + लॉग टैन 89°) - (लॉग कोस 1° + लॉग कोस 2° + ... + लॉग कोस 89°)
Detailed Solution for परीक्षा: त्रिकोणमिति- 2 - Question 7

समीकरण को इस प्रकार लिखते हैं :-

(लॉग साइन 1° - लॉग कोस 89°) + (लॉग साइन 2° - लॉग कोस 88°) + (लॉग साइन 3° - लॉग कोस 87°) ... + लॉग टैन 1°. लॉग टैन 89° + लॉग टैन 2°. लॉग टैन 88° + ...

=) (लॉग साइन 1° - लॉग साइन 1°) +(लॉग साइन 2° - लॉग साइन 2°)+ ... + लॉग टैन 1°कोट 1° + लॉग टैन 2°कोट 2°

=) लॉग 1 = 0
 

परीक्षा: त्रिकोणमिति- 2 - Question 8
Save

राम और श्याम 10 किमी की दूरी पर हैं। वे दोनों आकाश में उड़ते हुए एक गर्म हवा के गुब्बारे को देखते हैं, जो क्रमशः 60° और 30° के कोण पर है। गुब्बारा कितनी ऊंचाई पर उड़ रहा हो सकता है?
Detailed Solution for परीक्षा: त्रिकोणमिति- 2 - Question 8

परीक्षा: त्रिकोणमिति- 2 - Question 9
Save

एक आदमी जो एक टॉवर के ऊपर खड़ा है, एक कार को टॉवर की ओर आते हुए देखता है। यदि 30° से 60° के कोण के अवसरण में परिवर्तन होने में 20 मिनट लगते हैं, तो कार के टॉवर तक पहुंचने के लिए बचे समय की गणना करें?
Detailed Solution for परीक्षा: त्रिकोणमिति- 2 - Question 9

समाधान के लिए, हमें पहले टॉवर से कार की दूरी का अनुमान लगाना होगा। जब कोण अवसरण 30° है, तो हम इसे h मान सकते हैं। कार की दूरी D है। इस स्थिति में, D = h / tan(30°) और जब कोण 60° है, तो D = h / tan(60°)।

परीक्षा: त्रिकोणमिति- 2 - Question 10
Save

एक समकोण त्रिकोण की ऊँचाई ‘p’, आधार ‘b’ और कर्ण ‘h’ होता है। निम्नलिखित में से कौन सा मान h2 नहीं ले सकता, यह मानते हुए कि p और b धनात्मक पूर्णांक हैं?
Detailed Solution for परीक्षा: त्रिकोणमिति- 2 - Question 10

हमें पता है कि,
h2 = p2 + b2 दिया गया है, जहाँ p और b सकारात्मक पूर्णांक हैं, इसलिए h2 दो पूर्ण वर्गों का योग होगा। हम देखते हैं
a) 72 + 52 = 74 
b) 62 + 42 = 52
c) 32 + 22 = 13
d) दो पूर्ण वर्गों के योग के रूप में व्यक्त नहीं किया जा सकता
प्रश्न है "निम्नलिखित में से कौन-सी मान h2 नहीं ले सकती, यह मानते हुए कि p और b सकारात्मक पूर्णांक हैं?"
इसलिए, उत्तर है 23

171 docs|185 tests
Join Course
Information about परीक्षा: त्रिकोणमिति- 2 Page
In this test you can find the Exam questions for परीक्षा: त्रिकोणमिति- 2 solved & explained in the simplest way possible. Besides giving Questions and answers for परीक्षा: त्रिकोणमिति- 2, EduRev gives you an ample number of Online tests for practice
Download as PDF

Important Questions for परीक्षा: त्रिकोणमिति- 2

Find all the important questions for परीक्षा: त्रिकोणमिति- 2 at EduRev.Get fully prepared for परीक्षा: त्रिकोणमिति- 2 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the परीक्षा: त्रिकोणमिति- 2 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of परीक्षा: त्रिकोणमिति- 2 resources.

परीक्षा: त्रिकोणमिति- 2 MCQs with Answers

Prepare for the परीक्षा: त्रिकोणमिति- 2 within the Bank Exams exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for परीक्षा: त्रिकोणमिति- 2 Quantitative Aptitude/संख्यात्मक योग्यता

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace परीक्षा: त्रिकोणमिति- 2 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily