परीक्षा: मापन- 2 - CTET & State TET MCQ
10 Questions MCQ Test - परीक्षा: मापन- 2
एक क्यूबॉइड का आयतन निकालें जिसकी लंबाई 8 सेमी, चौड़ाई 6 सेमी और ऊँचाई 3.5 सेमी है।
एक क्यूबॉइड का आयतन ज्ञात करें जिसकी लंबाई 8 सेमी, चौड़ाई 3 सेमी और ऊँचाई 5 सेमी है।
वृत्त का क्षेत्रफल 2464 cm2 है और आयत की चौड़ाई का वृत्त के त्रिज्या के साथ अनुपात 6:7 है। यदि वृत्त का परिमाप आयत के परिमाप के बराबर है, तो आयत का क्षेत्रफल क्या होगा?
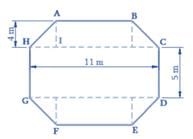
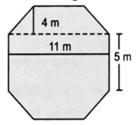
एक उठे हुए मंच की शीर्ष सतह नियमित अष्टकोण के आकार में है जैसा कि चित्र में दिखाया गया है। अष्टकोणीय सतह का क्षेत्रफल ज्ञात करें।
यदि एक समांतर चतुर्भुज की समांतर भुजाएँ 2 सेमी दूर हैं और उनका योग 10 सेमी है, तो उसका क्षेत्रफल क्या होगा?
यदि एक घन का किनारा 1 सेंटिमीटर है, तो निम्नलिखित में से इसका कुल सतह क्षेत्रफल क्या है?
एक त्रिभुज का क्षेत्रफल ज्ञात करें जिसका आधार 4 सेमी और ऊँचाई 6 सेमी है।
एक समांतर चतुर्भुज (रोम्बस) का क्षेत्रफल 200 सेमी² है, और इसकी एक विकर्ण 20 सेमी है। दूसरी विकर्ण की लंबाई _____ है।
घन के प्रत्येक पक्ष की लंबाई 24 सेमी है। घन का आयतन एक आयताकार घन के आयतन के बराबर है। यदि आयताकार घन की चौड़ाई और ऊँचाई क्रमशः 32 सेमी और 12 सेमी हैं, तो आयताकार घन की लंबाई क्या होगी?