All Courses
Get the App Signup / Login
Sign in Open App
Bank Exams Exam  >  Bank Exams Tests  >  General Intelligence & Reasoning (Hindi)  >  परीक्षा: वैन आरेख - 1 - Bank Exams MCQ

परीक्षा: वैन आरेख - 1 - Bank Exams MCQ


Test Description

10 Questions MCQ Test General Intelligence & Reasoning (Hindi) - परीक्षा: वैन आरेख - 1

परीक्षा: वैन आरेख - 1 for Bank Exams 2025 is part of General Intelligence & Reasoning (Hindi) preparation. The परीक्षा: वैन आरेख - 1 questions and answers have been prepared according to the Bank Exams exam syllabus.The परीक्षा: वैन आरेख - 1 MCQs are made for Bank Exams 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for परीक्षा: वैन आरेख - 1 below.
Solutions of परीक्षा: वैन आरेख - 1 questions in English are available as part of our General Intelligence & Reasoning (Hindi) for Bank Exams & परीक्षा: वैन आरेख - 1 solutions in Hindi for General Intelligence & Reasoning (Hindi) course. Download more important topics, notes, lectures and mock test series for Bank Exams Exam by signing up for free. Attempt परीक्षा: वैन आरेख - 1 | 10 questions in 20 minutes | Mock test for Bank Exams preparation | Free important questions MCQ to study General Intelligence & Reasoning (Hindi) for Bank Exams Exam | Download free PDF with solutions
परीक्षा: वैन आरेख - 1 - Question 1
Save

श्याम ने राम से अपनी संक्षिप्त छुट्टी के दौरान मुलाकात की। सुबह वे दोनों योग के लिए जाते थे। शाम को वे टेनिस खेलते थे। अधिक मजे के लिए, वे प्रतिदिन केवल एक गतिविधि में भाग लेते थे, अर्थात् या तो वे योग करने जाते थे या हर दिन टेनिस खेलते थे। ऐसे दिन भी थे जब वे आलसी थे और पूरे दिन घर पर रहे। ऐसे 24 सुबहें थीं जब उन्होंने कुछ नहीं किया, 14 शामें थीं जब वे घर पर रहे, और कुल 22 दिन थे जब उन्होंने योग किया या टेनिस खेला। श्याम ने राम के साथ कितने दिन बिताए?

Detailed Solution for परीक्षा: वैन आरेख - 1 - Question 1

मान लें कि छुट्टी के दिनों की संख्या x है।
उन्होंने x - 14 दिनों तक टेनिस खेला।
उन्होंने x - 24 दिनों तक योग किया।
तो, उन्होंने योग या टेनिस के लिए x - 14 + x - 24 = 2x - 38 दिनों तक किया।
2x – 38 = 22
=> x = 30

परीक्षा: वैन आरेख - 1 - Question 2
Save

100 ≤ n ≤ 200 के बीच कितने सम पूर्णांक n हैं, जो न तो सात से विभाज्य हैं और न ही नौ से?

Detailed Solution for परीक्षा: वैन आरेख - 1 - Question 2

100 और 200 के बीच (दोनों शामिल) 51 सम संख्या हैं।

7 सम संख्याएँ हैं जो 7 से विभाज्य हैं और 6 संख्याएँ हैं जो 9 से विभाज्य हैं, और 1 संख्या है जो दोनों से विभाज्य है, अर्थात् 42।

इसलिए कुल 51 - (7+6-1) = 39 हैं।

एक और तरीका है जिससे हम उत्तर पा सकते हैं।

चूंकि हमें सम संख्याएँ खोजनी हैं, 100 और 200 के बीच 14, 18 और 126 से विभाज्य संख्याओं पर विचार करें।

ये क्रमशः 7, 6 और 1 हैं।

Clear all your doubts with EduRev
परीक्षा: वैन आरेख - 1 - Question 3
Save

एक शहर में 3 क्लब A, B और C हैं जिनमें क्रमशः 40, 50 और 60 सदस्य हैं। जबकि 10 लोग सभी 3 क्लबों के सदस्य हैं, 70 केवल एक क्लब के सदस्य हैं। कितने लोग ठीक दो क्लबों के सदस्य हैं?

Detailed Solution for परीक्षा: वैन आरेख - 1 - Question 3

हमें पता है कि x + y + z = T और x + 2y + 3z = R, जहां
x = ठीक 1 सेट के सदस्य = 70
y = ठीक 2 सेट के सदस्य
z = ठीक 3 सेट के सदस्य = 10
T = कुल सदस्यों की संख्या
R = सभी सदस्यों की पुनरावृत्त कुल संख्या = (40 + 50 + 60) = 150
इसलिए हमारे पास दो समीकरण और दो अज्ञात हैं। इसे हल करने पर हमें y = 25 मिलता है।

तो, 25 लोग ठीक 2 क्लबों के सदस्य हैं।

परीक्षा: वैन आरेख - 1 - Question 4
Save

60 छात्रों की कक्षा में, अंग्रेजी एक सामान्य विषय के रूप में, छात्र गणित, भौतिकी, जीव विज्ञान या इनमें से किसी भी दो का प्रमुख विषय चुन सकते हैं। 6 छात्र गणित और भौतिकी दोनों में प्रमुख हैं, 15 छात्र भौतिकी और जीव विज्ञान दोनों में प्रमुख हैं, लेकिन कोई भी छात्र गणित और जीव विज्ञान दोनों में प्रमुख नहीं है। एक अंग्रेजी परीक्षा में, गणित में प्रमुख छात्रों द्वारा प्राप्त औसत अंक 45 हैं और जीव विज्ञान में प्रमुख छात्रों द्वारा प्राप्त औसत अंक 60 हैं। हालाँकि, इन दोनों प्रमुख विषयों के छात्रों का अंग्रेजी में संयुक्त औसत अंक 50 है। भौतिकी में केवल प्रमुख छात्रों की अधिकतम संभावित संख्या क्या है?
Detailed Solution for परीक्षा: वैन आरेख - 1 - Question 4

​​​​​

परीक्षा: वैन आरेख - 1 - Question 5
Save

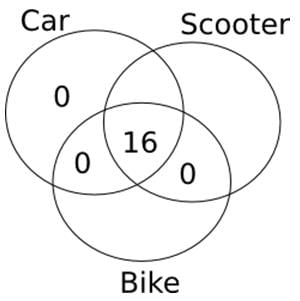
एक इमारत में रहने वाले 60 परिवारों में से, सभी परिवार जो एक कार के मालिक हैं, उनके पास एक स्कूटर भी है। कोई भी परिवार केवल एक स्कूटर और एक बाइक का मालिक नहीं है। 16 परिवारों के पास एक कार और एक बाइक दोनों हैं। प्रत्येक परिवार के पास कम से कम एक प्रकार का वाहन है और उन परिवारों की संख्या जो केवल एक प्रकार के वाहन के मालिक हैं, उन परिवारों की संख्या से अधिक है जो एक से अधिक प्रकार के वाहन के मालिक हैं। केवल एक बाइक के मालिक परिवारों की अधिकतम और न्यूनतम संख्या का योग क्या है?
Detailed Solution for परीक्षा: वैन आरेख - 1 - Question 5

प्रश्न में दिए गए जानकारी के आधार पर, निम्नलिखित वेन आरेख बनाया जा सकता है:

इसलिए, केवल बाइक रखने वाले परिवारों की संख्या को अधिकतम करने के लिए, हम शेष 44 परिवारों को 'केवल बाइक' क्षेत्र में रख सकते हैं।

इसी प्रकार, केवल बाइक रखने वाले परिवारों की संख्या को न्यूनतम करने के लिए, हम शेष 44 परिवारों को 'केवल स्कूटर' क्षेत्र में रख सकते हैं।

इसलिए, केवल बाइक रखने वाले परिवारों की अधिकतम संख्या 44 है और न्यूनतम संख्या 0 है।

इसलिए, योग = 44 + 0 = 44

परीक्षा: वैन आरेख - 1 - Question 6
Save

2018-19 MBA बैच में 400 छात्रों को प्रवेश दिया गया। इनमें से 200 ने “बिजनेस स्टैटिस्टिक्स” का चयन नहीं किया। 100 ने “इंटरनेशनल मैनेजमेंट” का चयन नहीं किया। 80 छात्र ऐसे थे जिन्होंने किसी भी दो विषयों का चयन नहीं किया। दोनों विषयों का चयन करने वाले छात्रों की संख्या ज्ञात करें।
Detailed Solution for परीक्षा: वैन आरेख - 1 - Question 6

जिन छात्रों ने बिजनेस स्टैटिस्टिक्स का चयन किया, उनकी संख्या = 400 − 200 = 200

जिन छात्रों ने इंटरनेशनल मैनेजमेंट का चयन किया, उनकी संख्या = 400 − 100 = 300

जिन छात्रों ने कम से कम एक विषय का चयन किया, उनकी संख्या = 400 − 80 = 320

अतः, दोनों विषयों का चयन करने वाले छात्रों की संख्या = 200 + 300 − 320 = 500 − 320 = 180

इसलिए, विकल्प (b) सही है।

परीक्षा: वैन आरेख - 1 - Question 7
Save

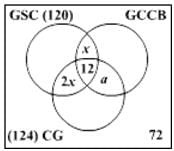
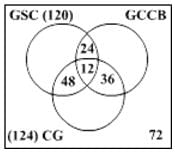
एक प्रमुख बी-स्कूल, जो एएसीएसबी मान्यता प्राप्त करने की प्रक्रिया में है, में 360 दूसरे वर्ष के छात्र हैं। अपने पाठ्यक्रम में स्थिरता को शामिल करने के लिए, इसने दूसरे वर्ष में तीन नए वैकल्पिक विषय पेश किए हैं, जिनमें ग्रीन सप्लाई चेन, वैश्विक जलवायु परिवर्तन और कॉर्पोरेट गवर्नेंस शामिल हैं। बारह छात्रों ने सभी तीन वैकल्पिक विषय लिए हैं, और 120 छात्र ग्रीन सप्लाई चेन का अध्ययन करते हैं। ऐसे छात्रों की संख्या जो ग्रीन सप्लाई चेन और कॉर्पोरेट गवर्नेंस का अध्ययन करते हैं लेकिन वैश्विक जलवायु परिवर्तन और व्यापार का नहीं करते, उन छात्रों की संख्या का दोगुना है जो ग्रीन सप्लाई चेन और वैश्विक जलवायु परिवर्तन और व्यापार का अध्ययन करते हैं लेकिन कॉर्पोरेट गवर्नेंस का नहीं करते, और उन सभी तीन विषयों का अध्ययन करने वाले छात्रों की संख्या का चार गुना है। 124 छात्र कॉर्पोरेट गवर्नेंस का अध्ययन करते हैं। 72 छात्र ऐसे हैं जिन्होंने इन विषयों में से कोई भी विषय लेने का साहस नहीं जुटाया। ग्रीन सप्लाई चेन और कॉर्पोरेट गवर्नेंस का अध्ययन करने वाले छात्रों का समूह ठीक उसी तरह का है जैसे वैश्विक जलवायु परिवर्तन और कॉर्पोरेट गवर्नेंस का अध्ययन करने वाले छात्रों का समूह। केवल कितने छात्र वैश्विक जलवायु परिवर्तन और व्यापार का अध्ययन करते हैं?
Detailed Solution for परीक्षा: वैन आरेख - 1 - Question 7

छात्रों की संख्या जो प्रत्येक विषय के संयोजन का अध्ययन करते हैं (प्रत्यक्ष डेटा के आधार पर) निम्नलिखित है:

यह दिया गया है: (ग्लोबल सप्लाई चेन और कॉर्पोरेट गवर्नेंस लेकिन ग्लोबल क्लाइमेट चेंज और बिजनेस) = 4 गुना (तीन वैकल्पिक)

अत: 2x = 4(12) अर्थात् x = 24

इसके अलावा: (ग्लोबल सप्लाई चेन और कॉर्पोरेट गवर्नेंस लेकिन ग्लोबल क्लाइमेट चेंज और बिजनेस) = (तीन वैकल्पिक) + (ग्लोबल क्लाइमेट चेंज और कॉर्पोरेट गवर्नेंस लेकिन ग्लोबल सप्लाई चेन)

अत: (ग्लोबल क्लाइमेट चेंज और कॉर्पोरेट गवर्नेंस लेकिन ग्लोबल सप्लाई चेन) = 2x - 12 = 2(24) - 12 = 36

तो, आंकड़ा इस प्रकार बनता है:

अब, कॉर्पोरेट गवर्नेंस केवल = 124 - (48 + 12 + 36) = 28

अत: ग्लोबल क्लाइमेट चेंज और बिजनेस अकेले = 360 - 120 - 36 - 28 - 72 = 104

इसलिए, विकल्प (b).

परीक्षा: वैन आरेख - 1 - Question 8
Save

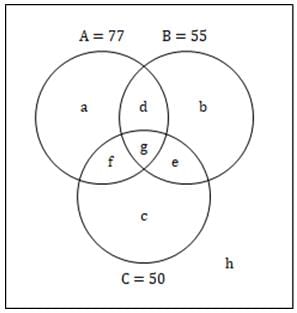
एक मनोरंजन पार्क में प्रवेश पास के साथ एक आगंतुक को तीन में से दो सवारी (A, B और C) मुफ्त मिलती हैं। एक विशेष दिन पर 77 लोगों ने सवारी A का चयन किया, 55 ने B का चयन किया और 50 ने C का चयन किया; 25 आगंतुकों ने A और C दोनों का चयन किया, 22 ने A और B दोनों का चयन किया, जबकि कोई भी आगंतुक B और C दोनों का चयन नहीं किया। 40 आगंतुकों ने सवारी A और B, या दोनों का चयन नहीं किया। उस दिन प्रवेश पास के साथ कुल कितने लोग आए?
Detailed Solution for परीक्षा: वैन आरेख - 1 - Question 8

वीन आरेख को चित्र में दिखाए अनुसार मान लें,

कोई भी तीनों सवारी नहीं ले सकता, इसलिए g = 0 है।

22 लोग सवारी A और B लेते हैं,
द = 22

25 लोग सवारी A और C लेते हैं,
फ = 25

50 लोग सवारी C लेते हैं,
c = 50 – 25 = 25 है।

40 लोग A या B या दोनों नहीं लेते हैं,
40 = c + h
⇒ h = 40 – 25 = 15

इसलिए, पार्क में आने वाले कुल लोगों की संख्या = (77 + 55 + 50 – 25 – 22) + 15 = 150।

इसलिए, विकल्प (d) है।

परीक्षा: वैन आरेख - 1 - Question 9
Save

290 छात्रों को MBA (अंतर्राष्ट्रीय व्यापार) में एक प्रतिष्ठित व्यवसाय स्कूल में त्रैमासिक IV और V में विदेशी भाषा का अध्ययन करना है। मान लीजिए कि निम्नलिखित जानकारी दी गई है।

(i) 120 छात्र स्पेनिश का अध्ययन करते हैं
(ii) 100 छात्र मंदारिन का अध्ययन करते हैं
(iii) कम से कम 80 छात्र, जो विदेशी भाषा का अध्ययन करते हैं, न तो स्पेनिश का अध्ययन करते हैं और न ही मंदारिन का

तो, स्पेनिश का अध्ययन करने वाले छात्रों की संख्या, जो मंदारिन का अध्ययन नहीं करते, कोई भी संख्या हो सकती है।
Detailed Solution for परीक्षा: वैन आरेख - 1 - Question 9

कम से कम 80 छात्र न तो स्पेनिश पढ़ते हैं और न ही मंदारिन।
इसलिए, कम से कम एक भाषा पढ़ने वाले छात्रों की अधिकतम संख्या = 290 – 80 = 210

दोनों भाषाएँ पढ़ने वाले छात्रों की न्यूनतम संख्या = 100 + 120 – 210 = 10

∴ स्पेनिश पढ़ने वाले, लेकिन मंदारिन नहीं पढ़ने वाले छात्रों की अधिकतम संख्या = 120 – 10 = 110

दोनों भाषाएँ पढ़ने वाले छात्रों की अधिकतम संख्या = 100 और 120 में से छोटी संख्या = 100

∴ स्पेनिश पढ़ने वाले, लेकिन मंदारिन नहीं पढ़ने वाले छात्रों की न्यूनतम संख्या = 120 – 100 = 20

इसलिए, यह संख्या 20 से 110 के बीच कोई भी हो सकती है।

इसलिए, विकल्प (a) है।

परीक्षा: वैन आरेख - 1 - Question 10
Save

एक निश्चित गाँव में, 22% परिवारों के पास कृषि भूमि है, 18% परिवारों के पास मोबाइल फोन है और 1600 परिवारों के पास कृषि भूमि और मोबाइल फोन दोनों हैं। यदि 68% परिवारों के पास न तो कृषि भूमि है और न ही मोबाइल फोन, तो गाँव में रहने वाले कुल परिवारों की संख्या है:
Detailed Solution for परीक्षा: वैन आरेख - 1 - Question 10

गाँव में कुल परिवारों की संख्या को T मान लें।
कृषि भूमि के मालिक परिवारों की संख्या, n(A) = 0.22T

मोबाइल फोन के मालिक परिवारों की संख्या, n(M) = 0.18T

कृषि भूमि और मोबाइल फोन दोनों के मालिक परिवारों की संख्या, n(A ⋂ M) = 1600

कृषि भूमि या मोबाइल फोन के मालिक परिवारों की संख्या, n(A ⋃ M) = T – 0.68T = 0.32T

अतः n(A ⋃ M) = n(A) + n(M) – n(A ⋂ M)

अतः n(A ⋂ M) = 0.08T

0.08T = 1600 ⟹ T = 20000

इसलिए, विकल्प (a)।

40 videos|127 docs|197 tests
Join Course
Information about परीक्षा: वैन आरेख - 1 Page
In this test you can find the Exam questions for परीक्षा: वैन आरेख - 1 solved & explained in the simplest way possible. Besides giving Questions and answers for परीक्षा: वैन आरेख - 1, EduRev gives you an ample number of Online tests for practice
Download as PDF

Important Questions for परीक्षा: वैन आरेख - 1

Find all the important questions for परीक्षा: वैन आरेख - 1 at EduRev.Get fully prepared for परीक्षा: वैन आरेख - 1 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the परीक्षा: वैन आरेख - 1 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of परीक्षा: वैन आरेख - 1 resources.

परीक्षा: वैन आरेख - 1 MCQs with Answers

Prepare for the परीक्षा: वैन आरेख - 1 within the Bank Exams exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for परीक्षा: वैन आरेख - 1 General Intelligence & Reasoning (Hindi)

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace परीक्षा: वैन आरेख - 1 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up
within 7 days!
Takes less than 10 seconds to signup