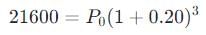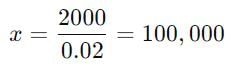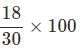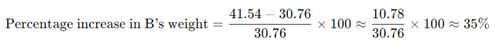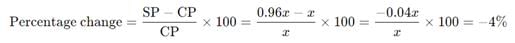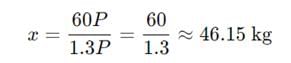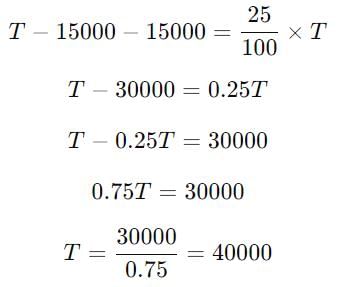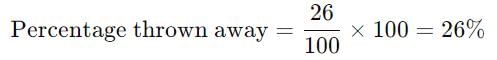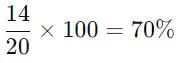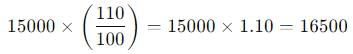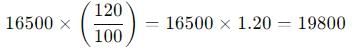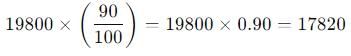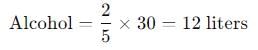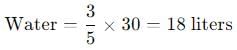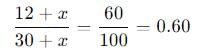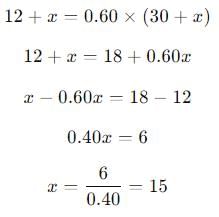Explore Exams
Login Signup
Sign in Open App
Bank Exams Exam  >  Bank Exams Tests  >  प्रतिशत - बहुविकल्पीय प्रश्न 3 - Bank Exams MCQ

प्रतिशत - बहुविकल्पीय प्रश्न 3 - Bank Exams MCQ


Test Description

20 Questions MCQ Test - प्रतिशत - बहुविकल्पीय प्रश्न 3

प्रतिशत - बहुविकल्पीय प्रश्न 3 for Bank Exams 2025 is part of Bank Exams preparation. The प्रतिशत - बहुविकल्पीय प्रश्न 3 questions and answers have been prepared according to the Bank Exams exam syllabus.The प्रतिशत - बहुविकल्पीय प्रश्न 3 MCQs are made for Bank Exams 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for प्रतिशत - बहुविकल्पीय प्रश्न 3 below.
Solutions of प्रतिशत - बहुविकल्पीय प्रश्न 3 questions in English are available as part of our course for Bank Exams & प्रतिशत - बहुविकल्पीय प्रश्न 3 solutions in Hindi for Bank Exams course. Download more important topics, notes, lectures and mock test series for Bank Exams Exam by signing up for free. Attempt प्रतिशत - बहुविकल्पीय प्रश्न 3 | 20 questions in 15 minutes | Mock test for Bank Exams preparation | Free important questions MCQ to study for Bank Exams Exam | Download free PDF with solutions
प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 1
Save

चावल की कीमत में 20% की कमी एक गृहिणी को 1200 रुपये में 5 किलोग्राम अधिक खरीदने की अनुमति देती है। चावल की प्रति किलोग्राम घटाई गई कीमत

Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 1

चरण-दर-चरण समाधान

  1. चर को परिभाषित करें:
    • मान लें कि p = चावल की प्रति किलोग्राम मूल कीमत (₹)
    • कम कीमत = मूल कीमत से 20% कम = 0.8p
  2. खरीदी गई मात्रा निर्धारित करें:
    • मूल कीमत पर:
      • खरीदी गई मात्रा = कुल धन / मूल कीमत = ₹1,200 / p = 1200/p किलोग्राम
    • कम कीमत पर:
      • खरीदी गई मात्रा = कुल धन / कम कीमत = ₹1,200 / (0.8p) = 1500/p किलोग्राम
  3. मात्रा में वृद्धि के आधार पर समीकरण स्थापित करें:
    • मात्रा में अंतर = 5 किलोग्राम
    • इसलिए, 1500/p - 1200/p = 5
    • समीकरण को सरल बनाएं:
      • 300/p = 5
    • p के लिए हल करें:
      • p = 300 / 5 = ₹60
  4. कम कीमत की गणना करें:
    • कम कीमत = 0.8 × मूल कीमत = 0.8 × ₹60 = ₹48

निष्कर्ष

चावल की प्रति किलोग्राम कम कीमत ₹48 है, जो कि विकल्प c) के अनुरूप है।

प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 2
Save

एक गाँव की जनसंख्या हर वर्ष 20% की दर से बढ़ी है। यदि 3 वर्षों के अंत में यह 21600 है, तो पहले वर्ष की शुरुआत में जनसंख्या कितनी थी?

Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 2

हम प्रारंभिक जनसंख्या ज्ञात करने के लिए यौगिक वृद्धि के सूत्र का उपयोग कर सकते हैं:

जहाँ:

  • P अंतिम जनसंख्या है (21600)
  • P0 प्रारंभिक जनसंख्या है (जिसे हम ज्ञात करना चाहते हैं)
  • r वार्षिक वृद्धि दर है (20% या 0.20)
  • n वर्षों की संख्या है (3)

ज्ञात मानों को डालें:

P0 के लिए सरल करें और हल करें:

  • 21600 = P0( 1.20)3
  • 21600 = P0( 12/10 x 12/10 x 12/10)
  • इसलिए, P0 = 12500
Clear all your doubts with EduRev
प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 3
Save

चुनाव में 12 प्रतिशत मतदाताओं ने अपना वोट नहीं डाला। इस चुनाव में केवल दो उम्मीदवार हैं। विजेता ने कुल वोटों का 45% प्राप्त करके जीत हासिल की और अपने प्रतिद्वंद्वी को 2000 वोटों से हराया। चुनाव में कुल वोटों की संख्या

Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 3

चुनाव में कुल मतदान संख्या को x मान लेते हैं।

12% मतदाताओं ने अपने मत नहीं डाले, इसलिए वैध मतों की संख्या कुल मतों का 88% है।

वैध मत = 0.88 × x

विजेता को कुल मतों का 45% मिला। इसलिए, विजेता द्वारा प्राप्त मत हैं:

0.45 × x

बाकी मत प्रतिकूल उम्मीदवार के लिए हैं, जो कि है:

0.88x − 0.45x = 0.43x मत

विजेता ने अपने प्रतिकूल को 2000 मतों से हराया। इसलिए, विजेता के मतों और प्रतिकूल के मतों के बीच का अंतर है:

0.45x − 0.43x = 2000

0.02x = 2000

x के लिए हल करें

प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 4
Save

एक संख्या को पहले 25% कम किया जाता है। फिर कम की गई संख्या को 20% बढ़ाया जाता है। परिणामी संख्या मूल संख्या से 40 कम है। फिर मूल संख्या है -
Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 4

मान लें कि मूल संख्या है x.

1. पहले, संख्या को 25% कम किया जाता है। तो, कम की गई संख्या बन जाती है:

कम की गई संख्या = x - (25/100) x = 0.75x

2. फिर कम की गई संख्या को 20% बढ़ाया जाता है। तो, परिणामी संख्या बन जाती है:

परिणामी संख्या = 0.75x + (20/100)(0.75x) = 0.75x + 0.15x = 0.9x

3. परिणामी संख्या मूल संख्या से 40 कम है:

x - 0.9x = 40

4. समीकरण को सरल बनाना:

0.1x = 40

5. x के लिए हल करना:

x = 40 / 0.1 = 400

इस प्रकार, मूल संख्या है 400.

प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 5
Save

सिनेमा हॉल में सीटों की संख्या 8% कम की गई है और साथ ही टिकट की कीमत 4% बढ़ाई गई है। इस परिवर्तन का राजस्व पर क्या प्रभाव पड़ेगा?
Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 5

दी गई जानकारी:

कमी की प्रतिशतता: 8%

बढ़ी हुई प्रतिशतता: 4%

उपयोग किया गया सूत्र:

प्रभावी प्रतिशत = x - y - (xy)/100

x = बढ़ी हुई प्रतिशतता

y = कमी की प्रतिशतता

गणना:

प्रभावी प्रतिशत = 4 - 8 - (4 × 8)/100

= - 4 - 0.32

= - 4.32%

-ve चिह्न का अर्थ है कमी की प्रतिशतता।

∴ सही उत्तर 4.32% की कमी है।

प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 6
Save

अश्विन ने 30 मिठाइयाँ श्वेता और पल्लवी के बीच 2 : 3 के अनुपात में बाँटीं। पल्लवी को मिठाइयों का कितना प्रतिशत मिलता है?
Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 6

कुल मिठाइयाँ = 30

श्वेता और पल्लवी को मिली मिठाइयों का अनुपात 2 : 3 है

मान लेते हैं कि अनुपात गुणांक x है।

तो, श्वेता को मिली मिठाइयाँ = 2x

और पल्लवी को मिली मिठाइयाँ = 3x

कुल मिठाइयाँ = 2x + 3x = 5x

लेकिन दिया गया है कि

5x = 30

इसलिए, x = 30/5 = 6

तो, श्वेता को मिली मिठाइयाँ = 2 × 6 = 12

और पल्लवी को मिली मिठाइयाँ = 3 × 6 = 18

पल्लवी को मिली मिठाइयों का प्रतिशत = 60%

प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 7
Save

दो दोस्तों A और B का वजन 1 : 2 के अनुपात में है। A का वजन 20% बढ़ जाता है और A और B का कुल वजन 60 किलोग्राम हो जाता है, जिसमें 30% का वृद्धि होती है। B का वजन कितने प्रतिशत बढ़ा?
Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 7

मान लीजिए कि A और B का मूल वजन क्रमशः A और B है। चूंकि उनके वजन का अनुपात 1 : 2 है, हम कह सकते हैं:

A = x और B = 2x

A का वजन 20% बढ़ जाता है, इसलिए A का नया वजन है:

नया वजन A = A + 20% का A = x + 0.20x = 1.2x

वजन बढ़ने के बाद A और B का कुल वजन 60 किलोग्राम है, और यह भी दिया गया है कि कुल वजन 30% बढ़ा है। इसलिए, A और B का मूल कुल वजन था:

मूल कुल वजन = 60/1.30 = 46.15 किलोग्राम (लगभग)

चूंकि A और B का मूल कुल वजन भी A + B = x + 2x = 3x है, तो:

3x = 46.15 ⇒ x = 46.15/3 = 15.38 किलोग्राम (लगभग)

तो, A का मूल वजन लगभग 15.38 किलोग्राम है, और B का मूल वजन है:

B = 2x = 2 × 15.38 = 30.76 किलोग्राम (लगभग)

नया कुल वजन 60 किलोग्राम है, और A का नया वजन 1.2x = 1.2 × 15.38 = 18.46 किलोग्राम है। इसलिए, B का नया वजन है:

नया वजन B = 60 - 18.46 = 41.54 किलोग्राम (लगभग)

अब, हम B के वजन में प्रतिशत वृद्धि की गणना कर सकते हैं:

इसलिए, B का वजन 35% बढ़ा है।

प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 8
Save

एक लेख का अंकित मूल्य लागत मूल्य से 20% अधिक है। अंकित मूल्य पर 20% छूट दी जाती है। इस लेन-देन में विक्रेता
Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 8
  • लेख की लागत मूल्य (CP) को x मान लेते हैं।
  • निशान मूल्य (MP) लागत मूल्य से 20% अधिक है, इसलिए:
  • निशान मूल्य (MP) = x + 20% of x = x + 0.20x = 1.2x
  • निशान मूल्य पर 20% की छूट दी जाती है।
  • छूट के बाद बिक्री मूल्य (SP) है:
  • बिक्री मूल्य (SP) = MP − 20% of MP = 1.2x − 0.20 × 1.2x = 1.2x − 0.24x = 0.96x
  • अब, बिक्री मूल्य (SP) की तुलना लागत मूल्य (CP) से करें:
  • बिक्री मूल्य 0.96x है, और लागत मूल्य x है।
  • प्रतिशत हानि या लाभ की गणना इस प्रकार की जा सकती है:
  • इस प्रकार, विक्रेता को इस लेनदेन में 4% की हानि होती है।
प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 9
Save

जब चावल की कीमत 30 प्रतिशत बढ़ जाती है, तो एक परिवार अपनी खपत को इस प्रकार कम कर देता है कि खर्च पहले से केवल 20 प्रतिशत अधिक होता है। यदि परिवार पहले 50 किलोग्राम चावल का सेवन करता है, तो परिवार की नई खपत (लगभग) क्या होगी?
Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 9

मान लेते हैं कि चावल की मूल कीमत है P (प्रति किलोग्राम)।

परिवार द्वारा चावल की मूल खपत 50 किलोग्राम है।

परिवार का मूल खर्च है:

मूल खर्च = 50 × P = 50P

चावल की कीमत 30% बढ़ जाती है।

चावल की नई कीमत होती है:

नई कीमत = P + 30%  का P = P + 0.30P = 1.3P

परिवार का खर्च 20% बढ़ता है।

नई खर्च:

नई खर्च = 50P + 20%  का 50P = 50P + 0.20 × 50P = 60P

मान लेते हैं कि चावल की नई खपत है x किलोग्राम.

नई खर्च नई कीमत और नई खपत का गुणनफल है:

नई खर्च = x × 1.3P

नई खर्च को पिछले खर्च के 60P के बराबर निर्धारित करें:

x × 1.3P = 60P

इसलिए, परिवार की नई खपत लगभग 46 किलोग्राम है।

प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 10
Save

एक व्यक्ति के खाते में दो वर्ष पूर्व 4000 रुपये थे। पहले वर्ष उसने अपने खाते में राशि का 20 प्रतिशत जमा किया। अगले वर्ष उसने बढ़ी हुई राशि का 10 प्रतिशत खाते में जमा किया। व्यक्ति के खाते में 2 वर्षों के बाद कुल राशि ज्ञात कीजिए।
Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 10

दिया गया:

  • एक व्यक्ति के खाते में दो वर्ष पूर्व 4000 रुपये थे।
  • पहले वर्ष उसने अपने खाते में 20% जमा किया।
  • अगले वर्ष उसने बढ़ी हुई राशि का 10% जमा किया।
  • गणना:
  • पहले वर्ष में,
  • उसका जमा = 20% × 4000 = 800 रुपये
  • अतः पहले वर्ष के बाद बढ़ी हुई राशि = 4000 + 800 = 4800 रुपये
  • अगले वर्ष,
  • उसका जमा = 10% × 4800 = 480 रुपये
  • अतः व्यक्ति के खाते में 2 वर्षों के बाद कुल राशि = 4800 + 480
  • = 5280 रुपये
  • अतः व्यक्ति के खाते में 2 वर्षों के बाद कुल राशि = 5280 रुपये
प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 11
Save

एक चुनाव में जिसमें दो पार्टियाँ A और B शामिल थीं, पार्टी A ने पार्टी B की तुलना में कुल वोटों का 25 प्रतिशत अधिक प्राप्त किया। यदि पार्टी B को 15000 वोट मिले हैं, तो पार्टी B चुनाव में कितने वोटों से हारती है?
Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 11
  • कुल मतों की संख्या को T मान लें।
  • पार्टी B को 15,000 वोट मिलते हैं।
  • समस्या के अनुसार, पार्टी A को पार्टी B से 25% अधिक वोट मिले हैं। इसलिए, पार्टी A के लिए वोटों की संख्या T - 15000 है, और यह भी पार्टी B के वोटों से 25% अधिक है, जिसका मतलब है:
  • इसलिए, कुल वोटों की संख्या 40,000 है।
  • पार्टी A के वोट = T - 15000 = 40000 - 15000 = 25000।
  • पार्टी B के वोट = 15,000 (जैसा कि दिया गया है)।
  • पार्टी A और पार्टी B के वोटों के बीच का अंतर है:
  • 25000 - 15000 = 10000
  • इस प्रकार, पार्टी B 10,000 वोटों से चुनाव हार जाती है।
प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 12
Save

एक विक्रेता अपने पास मौजूद सेबों का 50 प्रतिशत बेचता है और शेष का 20 प्रतिशत फेंक देता है। अगले दिन वह शेष का 60 प्रतिशत बेचता है और बाकी फेंक देता है। विक्रेता अपने सेबों का कितना प्रतिशत फेंकता है?
Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 12

मान लीजिए कि विक्रेता के पास शुरू में कुल 100 सेब थे (सरलता के लिए)।

पहले दिन:

विक्रेता सेबों का 50% बेचता है:

पहले दिन बेचे गए सेब = 50% का 100 = 50

50% बेचने के बाद शेष सेब हैं:

शेष सेब = 100 - 50 = 50

वह फिर शेष सेबों का 20% फेंक देता है:

पहले दिन फेंके गए सेब = 20% का 50 = 10

20% फेंकने के बाद शेष सेब हैं:

पहले दिन के बाद शेष सेब = 50 - 10 = 40

दूसरे दिन:

विक्रेता शेष सेबों का 60% बेचता है:

दूसरे दिन बेचे गए सेब = 60% का 40 = 24

60% बेचने के बाद शेष सेब हैं:

दूसरे दिन बेचने के बाद शेष सेब = 40 - 24 = 16

वह बाकी को फेंक देता है, जो कि 16 सेब हैं।

कुल फेंके गए सेब:

पहले दिन फेंके गए सेब = 10

दूसरे दिन फेंके गए सेब = 16

कुल फेंके गए सेब = 10 + 16 = 26

फेंके गए सेबों का प्रतिशत:

इस प्रकार, विक्रेता अपने सेबों का 26% फेंकता है।

प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 13
Save

महिलाओं में से 40% 30 वर्ष से अधिक हैं और 80 प्रतिशत महिलाएं 50 वर्ष से कम या समान हैं। सभी महिलाओं में से 20 प्रतिशत बास्केटबॉल खेलती हैं। यदि 50 वर्ष से ऊपर की महिलाओं में से 30 प्रतिशत बास्केटबॉल खेलती हैं, तो 50 वर्ष से कम या समान खिलाड़ियों का प्रतिशत क्या है?
Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 13

मान लें कि महिलाओं की कुल संख्या 100 है (सरलता के लिए)।

30 वर्ष से अधिक महिलाएं:

महिलाओं में से 40% 30 वर्ष से अधिक हैं, जिसका अर्थ है:

30 वर्ष से अधिक महिलाएं = 40% × 100 = 40 महिलाएं

50 वर्ष से कम या समान महिलाएं:

महिलाओं में से 80% 50 वर्ष से कम या समान हैं, जिसका अर्थ है:

50 वर्ष से कम या समान महिलाएं = 80% × 100 = 80 महिलाएं

50 वर्ष से अधिक महिलाएं:

चूंकि 80% 50 वर्ष से कम हैं, शेष 20% 50 वर्ष से अधिक हैं, जिसका अर्थ है:

50 वर्ष से अधिक महिलाएं = 20% × 100 = 20 महिलाएं

बास्केटबॉल खेलने वाली महिलाएं:

सभी महिलाओं में से 20% बास्केटबॉल खेलती हैं, जिसका अर्थ है:

कुल बास्केटबॉल खिलाड़ी = 20% × 100 = 20 महिलाएं

50 वर्ष से अधिक की महिलाएं जो बास्केटबॉल खेलती हैं:

50 वर्ष से ऊपर की महिलाओं में से 30% बास्केटबॉल खेलती हैं, जिसका अर्थ है:

50 वर्ष से ऊपर की बास्केटबॉल खिलाड़ी = 30% × 20 = 6 महिलाएं

50 वर्ष से कम या समान की महिलाएं जो बास्केटबॉल खेलती हैं:

कुल बास्केटबॉल खिलाड़ियों की संख्या 20 है, और उनमें से 6 50 वर्ष से अधिक हैं।

इसलिए, 50 वर्ष से कम या समान खिलाड़ियों की संख्या है:

50 वर्ष से कम या समान बास्केटबॉल खिलाड़ी = 20 − 6 = 14 महिलाएं

50 वर्ष से कम या समान खिलाड़ियों का प्रतिशत:

50 वर्ष से कम या समान खिलाड़ियों का प्रतिशत = (14/20) × 100 = 70%

इस प्रकार, बास्केटबॉल खिलाड़ियों में से 70% 50 वर्ष से कम या समान हैं।

प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 14
Save

अलीशा एक सुपरमार्केट गई और 60 रुपये की चीजें खरीदीं, जिनमें से 40 पैसे बिक्री कर में गए। यदि कर की दर 10 प्रतिशत है, तो कर मुक्त सामान की लागत क्या थी?
Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 14
  • वस्तुओं की कुल लागत = ₹60
  • भुगतान किया गया बिक्री कर = 40 पैसे = ₹0.40
  • कर की दर = 10%। इसलिए, कर की राशि कराधीन वस्तुओं की लागत का 10% है (जिसे T के रूप में दर्शाया गया है)।
  • बिक्री कर का समीकरण है:
  • T के लिए हल करना:
  • अब, कर-मुक्त वस्तुओं की लागत है:
  • कर-मुक्त वस्तुओं की लागत = 60 − T − बिक्री कर = 60 − 4 − 0.40 = 55.60 रुपये।
  • इस प्रकार, कर-मुक्त वस्तुओं की लागत ₹55.60 है।
प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 15
Save

किसी कंपनी के 60 प्रतिशत कर्मचारी महिलाएँ हैं और 75% महिलाएँ महीने में 20000 या उससे अधिक कमाती हैं। कंपनी में महीने में 20000 से अधिक कमाने वाले कर्मचारियों की कुल संख्या कुल कर्मचारियों का 60 प्रतिशत है। कितने प्रतिशत पुरुष महीने में 20000 से कम कमाते हैं?
Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 15

कुल कर्मचारी = 100 (सरलता के लिए)।

महिलाओं की संख्या = 100 का 60% = 60 महिलाएँ।

पुरुषों की संख्या = 100 का 40% = 40 पुरुष।

75% महिलाएँ 20,000 या उससे अधिक कमाती हैं:

महिलाएँ जो 20,000 या उससे अधिक कमाती हैं = 60 का 75% = 0.75 × 60 = 45 महिलाएँ।

कुल कर्मचारी जो महीने में 20,000 से अधिक कमाते हैं, वे कुल कर्मचारियों का 60% हैं:

20,000 से अधिक कमाने वाले कर्मचारी = 100 का 60% = 60 कर्मचारी।

इन 60 कर्मचारियों में से 45 महिलाएँ हैं, इसलिए शेष 15 पुरुष होने चाहिए:

20,000 से अधिक कमाने वाले पुरुष = 15 पुरुष।

पुरुषों की कुल संख्या 40 है, और 15 पुरुष 20,000 से अधिक कमाते हैं, इसलिए 20,000 से कम कमाने वाले पुरुषों की संख्या:

20,000 से कम कमाने वाले पुरुष = 40 − 15 = 25 पुरुष।

20,000 से कम कमाने वाले पुरुषों का अंश:

अंश = 25/40 = 5 / 8

इसलिए, सही उत्तर है A: 5/8

प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 16
Save

एक पुस्तकालय में, 30% पुस्तकें इतिहास में हैं। शेष पुस्तकों का 50% अंग्रेजी में है और शेष का 40% जर्मन में है। शेष 4200 पुस्तकें क्षेत्रीय भाषाओं में हैं। पुस्तकालय में पुस्तकों की कुल संख्या क्या है?
Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 16

पुस्तकालय में पुस्तकों की कुल संख्या को टी मान लेते हैं।

इतिहास में 30% पुस्तकें हैं:

इतिहास की पुस्तकें = 30% टी = 0.30 × टी

इतिहास को ध्यान में रखते हुए शेष पुस्तकें हैं:

शेष पुस्तकें = टी - 0.30 × टी = 0.70 × टी

शेष पुस्तकों का 50% अंग्रेजी में है:

अंग्रेजी की पुस्तकें = 50% शेष = 0.50 × 0.70 × टी = 0.35 × टी

अंग्रेजी की पुस्तकों को ध्यान में रखते हुए शेष पुस्तकें हैं:

अंग्रेजी के बाद शेष पुस्तकें = 0.70टी - 0.35टी = 0.35टी

शेष पुस्तकों का 40% जर्मन में है:

जर्मन की पुस्तकें = 40% शेष = 0.40 × 0.35 × टी = 0.14 × टी

जर्मन की पुस्तकों को ध्यान में रखते हुए शेष पुस्तकें हैं:

जर्मन के बाद शेष पुस्तकें = 0.35टी - 0.14टी = 0.21टी

शेष 4200 पुस्तकें क्षेत्रीय भाषाओं में हैं, इसलिए:

0.21 × टी = 4200

टी के लिए हल करना:

टी = 4200/0.21 = 20000

इसलिए, पुस्तकालय में पुस्तकों की कुल संख्या 20,000 है।

प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 17
Save

A ने एक परीक्षा में अधिकतम अंकों का 30% प्राप्त किया और 10 अंकों से असफल रहा। हालाँकि, B ने उसी परीक्षा में कुल अंकों का 40% प्राप्त किया और उत्तीर्ण अंकों से 15 अंक अधिक प्राप्त किए। परीक्षा में उत्तीर्ण अंक क्या थे?
Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 17

मान लीजिए परीक्षा में अधिकतम अंक 100x हैं और उत्तीर्ण अंक y हैं।

A ने अधिकतम अंकों का 30% प्राप्त किया, यानी 30x + 10 = y -----------(i)

इसी तरह, B के लिए 40x - 15 = y -------(ii)

समीकरण (i) को (ii) से घटाने पर, 10x = 25

=> x = 2.5

(ii) में इसे प्रतिस्थापित करने पर, हमें मिलता है: उत्तीर्ण अंक y = 85।

प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 18
Save

एक शहर की जनसंख्या 15000 है। यह पहले वर्ष में 10 प्रतिशत बढ़ती है और दूसरे वर्ष में 20 प्रतिशत बढ़ती है। लेकिन तीसरे वर्ष में यह 10 प्रतिशत घट जाती है। तीन वर्षों के बाद जनसंख्या क्या होगी?
Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 18

प्रारंभिक जनसंख्या = 15000।

पहले वर्ष: जनसंख्या 10% बढ़ती है।

पहले वर्ष के बाद नई जनसंख्या:

दूसरे वर्ष: जनसंख्या 20% बढ़ती है।

दूसरे वर्ष के बाद नई जनसंख्या:

तीसरे वर्ष: जनसंख्या 10% घटती है।

तीसरे वर्ष के बाद नई जनसंख्या:

इस प्रकार, तीन वर्षों के बाद जनसंख्या 17820 होगी।

प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 19
Save

30 लीटर के घोल में शराब और पानी का अनुपात 2:3 है। घोल में कितना शराब मिलाना चाहिए ताकि शराब का प्रतिशत 60% हो जाए?
Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 19

प्रारंभिक घोल में 30 लीटर हैं, जिसमें शराब और पानी का अनुपात 2:3 है। घोल में शराब की मात्रा है: 12 लीटर। घोल में पानी की मात्रा है: 18 लीटर। हमें शराब की कुछ मात्रा (मान लेते हैं, इसे x) मिलानी होगी ताकि शराब का प्रतिशत कुल घोल का 60% हो जाए। जब हम x लीटर शराब मिलाते हैं, तो नया कुल घोल का मात्रा 30 + x लीटर होगा, और शराब की मात्रा 12 + x लीटर होगी। शराब की सांद्रता 60% होनी चाहिए, इसलिए: (12 + x) / (30 + x) = 0.6। समीकरण हल करने पर: हमें 15 लीटर शराब मिलानी होगी।

प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 20
Save

720 मिठाइयाँ बच्चों में इस तरह बाँटी गई हैं कि प्रत्येक बच्चे को दी गई मिठाइयों की संख्या कुल बच्चों की संख्या का 20% है। प्रत्येक बच्चे को कितनी मिठाइयाँ मिलीं?
Detailed Solution for प्रतिशत - बहुविकल्पीय प्रश्न 3 - Question 20

दिया गया,

कुल मिठाइयाँ = 720

संकल्पना:

x% किसी भी मान का = वास्तविक मान × (x/100)

गणना:

मान लें बच्चों की संख्या x है, तो

प्रत्येक बच्चे को मिलने वाली मिठाइयों की संख्या = x × (20/100)

प्रश्न के अनुसार

x × x × 20/100 = 720

⇒ x2/5 = 720

⇒ x2 = 720 × 5

⇒ x2 = 3600

⇒ x = √3600

⇒ x = 60

∴ प्रत्येक बच्चे को मिलने वाली मिठाइयाँ = 60/5 = 12

Information about प्रतिशत - बहुविकल्पीय प्रश्न 3 Page
In this test you can find the Exam questions for प्रतिशत - बहुविकल्पीय प्रश्न 3 solved & explained in the simplest way possible. Besides giving Questions and answers for प्रतिशत - बहुविकल्पीय प्रश्न 3, EduRev gives you an ample number of Online tests for practice
Download as PDF

Important Questions for प्रतिशत - बहुविकल्पीय प्रश्न 3

Find all the important questions for प्रतिशत - बहुविकल्पीय प्रश्न 3 at EduRev.Get fully prepared for प्रतिशत - बहुविकल्पीय प्रश्न 3 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the प्रतिशत - बहुविकल्पीय प्रश्न 3 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of प्रतिशत - बहुविकल्पीय प्रश्न 3 resources.

प्रतिशत - बहुविकल्पीय प्रश्न 3 MCQs with Answers

Prepare for the प्रतिशत - बहुविकल्पीय प्रश्न 3 within the Bank Exams exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for प्रतिशत - बहुविकल्पीय प्रश्न 3

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace प्रतिशत - बहुविकल्पीय प्रश्न 3 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup