प्रैक्टिस टेस्ट: गणित शिक्षा पद्धति - 1 - CTET & State TET MCQ
30 Questions MCQ Test - प्रैक्टिस टेस्ट: गणित शिक्षा पद्धति - 1
गणित पढ़ाने की प्रारंभिक अवस्था कौन सी है?
गणित की कौन सी तकनीकें गणित में गति और सटीकता में सुधार करती हैं?
खेलते समय रम चार डंडों से एक चतुष्भुज बनाता है और एक कॉपी में निम्नलिखित तालिका बनाता है:
चतुष्भुजों की संख्या 1 2 3
डंडों की संख्या 4 8 12
उसकी क्रिया से कौन सा निष्कर्ष निकाला जा सकता है?
डंडों की संख्या 4 8 12
गणित के छात्रों का पोर्टफोलियो क्या हो सकता है?
कौन सी स्केल अंतराल स्केल की विशेषताओं को दर्शाती है?
________ बच्चे वे बच्चे हैं जो अपनी बौद्धिक वृद्धि और विकास के मामले में औसत से बहुत ऊपर हैं।
पांच चरणों की पाठ योजना प्रणाली किसने शुरू की?
जब शिक्षक 'आकृतियों' का शिक्षण कर रहे होते हैं, तो वे ऐतिहासिक स्थलों की यात्रा की योजना कैसे बना सकते हैं?
बच्चों में गिनती के कौशल को विकसित करने के लिए, निम्नलिखित में से कौन सी पूर्व संख्या अवधारणा के रूप में सीखने की आवश्यकता नहीं है?
निम्नलिखित आकृति में कितने आयत हैं?
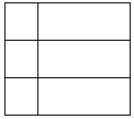
उपरोक्त प्रश्न छात्र के ज्ञान का परीक्षण कर रहा है।
फरहान स्कूल की पुस्तकालय में गया और पाया कि कहानी अनुभाग में रखी 100 पुस्तकें खराब हो गई हैं। 20 पुस्तकें गायब हैं। 219 पुस्तकें शेल्फ में रखी हैं और 132 छात्रों को जारी की गई हैं। पुस्तकालय में कुल कितनी कहानी की पुस्तकें थीं? इस प्रश्न के माध्यम से शिक्षक निम्नलिखित मूल्य सिखा सकते हैं
किसी कक्षा के स्तर के अनुसार सामग्री के विकार का निदान करने के लिए ____।
NCF 2005 के अनुसार
“बच्चों की गणितीकरण की क्षमताओं का विकास गणित शिक्षा का मुख्य लक्ष्य है। स्कूल गणित का संकीर्ण उद्देश्य 'उपयोगी' क्षमताओं का विकास करना है।”
यहाँ गणितीकरण का तात्पर्य है बच्चे की क्षमताओं का विकास करना।
निम्नलिखित में से कौन सा अनुशासनात्मक शिक्षण का कार्य नहीं है?
सलमान ने हल किया - 3 – 4 = 7। यह त्रुटि की गई है
एक कक्षा में छात्रों से ऊर्ध्वाधर विपरीत कोणों के बीच संबंध स्थापित करने के लिए कहा गया। वे विभिन्न आकृतियाँ बनाते हैं, कोणों को मापते हैं और देखते हैं कि ऊर्ध्वाधर विपरीत कोण समान होते हैं। इस मामले में, छात्रों का सीखना वान हीले के अनुसार किस स्तर पर है?
गणित शिक्षा का पाठ्यक्रम में स्थान दो मुख्य चिंताओं पर आधारित है:
वस्तुनिष्ठ प्रकार के परीक्षण की सबसे महत्वपूर्ण विशेषताएँ क्या हैं?
यदि एक शिक्षक को अंकगणित में "संयुक्त ब्याज" विषय पढ़ाना है, तो इसके अध्ययन के उद्देश्यों को निम्नलिखित होना चाहिए:
निर्देश: निम्नलिखित प्रश्न का उत्तर सही/सबसे उपयुक्त विकल्प चुनकर दें: निम्नलिखित में से "संख्या समझ" का एक पहलू कौन सा है?
निर्देश: निम्नलिखित प्रश्न का उत्तर सही/सबसे उपयुक्त विकल्प चुनकर दें:
एक शिक्षक कक्षा I में 'संख्याएँ' विषय पर शिक्षार्थियों के साथ चर्चा कर रहे हैं। निम्नलिखित में से कौन सा दृष्टिकोण शिक्षक द्वारा अपनाया जाना सबसे उपयुक्त है?
कौन सा अध्ययन सुधारात्मक शिक्षण के लिए आसिमिलेशन के रूप में जाना जाता है?
एक शिक्षक ने छात्रों से पत्तियाँ इकट्ठा करने और सममिति पैटर्न की पहचान करने के लिए कहा। यह कार्य शिक्षक के प्रयासों को दर्शाता है
जब 'आकृतियों' की शिक्षा दी जाती है, तो एक शिक्षक ऐतिहासिक स्थलों की यात्रा की योजना कैसे बना सकता है?
नीचे कक्षा V की पाठ्यपुस्तक से एक समस्या दी गई है: "चार खंभे हैं जिनकी लंबाई क्रमशः 105 सेंटीमीटर, 115 सेंटीमीटर, 150 सेंटीमीटर और 235 सेंटीमीटर है। यदि इन्हें समान लंबाई के टुकड़ों में काटा जाना है, तो प्रत्येक टुकड़े की अधिकतम लंबाई क्या होगी?" यह प्रश्न पूछा गया है
यदि एक बच्चा यह पहचानता है कि 'सभी वर्ग आयत हैं, लेकिन सभी आयत वर्ग नहीं हैं', तो उस बच्चे में कौन सी विशेषता है?
निर्देश: सही / सबसे उपयुक्त विकल्प चुनकर निम्नलिखित प्रश्न का उत्तर दें।
निम्नलिखित में से कौन सा कथन सत्य नहीं है गणितीय प्रमेय के बारे में?
निर्देश:निम्नलिखित प्रश्न का उत्तर सही / सबसे उपयुक्त विकल्प चुनकर दें।
इस प्रमेय पर विचार करें –
“यदि 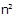 विषम है, तो n विषम है।”
विषम है, तो n विषम है।”
इसे इस तरह से सिद्ध किया जा सकता है:














