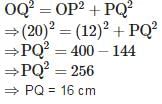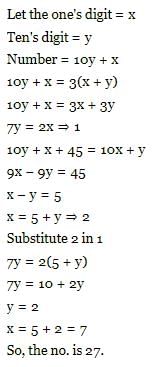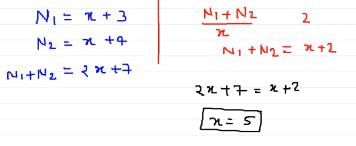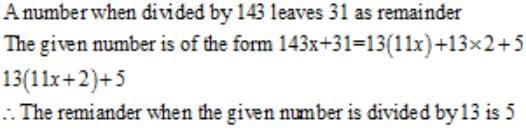सीटीईटी अभ्यास परीक्षा: गणित - 5 - CTET & State TET MCQ
30 Questions MCQ Test - सीटीईटी अभ्यास परीक्षा: गणित - 5
प्रत्येक बार की ________ आवश्यक जानकारी प्रदान करती है।
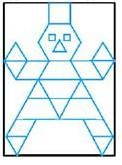
नीचे दिए गए आकृति में समान्तर रेखाओं की संख्या ज्ञात करें:

एक वृत्त पर संपर्क बिंदु P पर एक टेन्जेंट PQ है, जो केंद्र O के माध्यम से एक रेखा से मिलती है, इस प्रकार OQ = 20 सेमी है, टेन्जेंट PQ की लंबाई क्या है?
एक निश्चित दो अंकों की संख्या उसके अंकों के योग के तीन गुना है। यदि इसमें 45 जोड़ा जाए, तो अंकों का स्थान उलट जाता है। वह संख्या _______ है।
संख्याओं 428721 में दो 2 के स्थान मान का गुणनफल क्या है?
गुणनखंड ABCD में, ∠B=90∘, ∠C−∠D = 60∘ और ∠A−∠C−∠D = 10∘ है। ∠A, ∠C और ∠D ज्ञात करें।
यदि x + y = -10 और xy = 16 है, तो निम्नलिखित में से कौन-सी बात सच होनी चाहिए?
(I) x – y = -6
(II) x2 + y2 = 68
(III) (x-y)2 को 7 से भाग देने पर शेषफल 1 आता है
समान त्रिकोणों, ABC और DEF का क्षेत्रफल क्रमशः 144 cm2 और 81 cm2 है। यदि बड़े त्रिकोण ABC की सबसे लंबी भुजा 36 cm है, तो छोटे त्रिकोण DEF की सबसे लंबी भुजा क्या होगी?
यदि दो संख्याएँ एक ही भाजक से विभाजित की जाती हैं, तो शेषफल क्रमशः 3 और 4 होते हैं। यदि दोनों संख्याओं का योग उसी भाजक से विभाजित किया जाए, तो शेषफल 2 होता है। भाजक क्या है?
एक संख्या को 2, 3, 4, 5 या 6 से विभाजित किया जाता है, प्रत्येक मामले में शेषफल एक होता है। लेकिन संख्या 7 से पूरी तरह विभाज्य है। यह संख्या 250 और 350 के बीच है, इस संख्या के अंकों का योग होगा
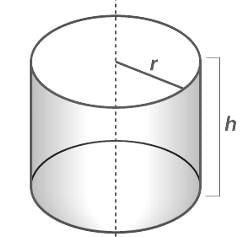
एक सही गोलाकार सिलेंडर में, गोल चेहरे के केंद्र को जोड़ने वाले रेखा खंड आधार के ________ हैं।
नियमित षट्कोण में समरूपता की रेखाओं की संख्या ज्ञात करें।
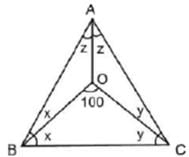
त्रिकोण ABC में, अंतः केन्द्र 0 पर है। यदि ㄥBOC = 100°, तो ㄥBAC ज्ञात करें।
A 5वां अभाज्य संख्या है। B 7वां अभाज्य संख्या है। B - A क्या है?
एक त्रिकोण ABC का निर्माण, यह दिया गया है कि BC = 6 सेमी, B = ∠45° तब संभव नहीं है जब AB और AC का अंतर बराबर हो:
X और Y की मासिक आय का अनुपात 4:3 है और उनके मासिक व्यय का अनुपात 3:2 है। हालांकि, प्रत्येक महीने 6000 रुपये बचाते हैं। उनकी कुल मासिक आय क्या है?
अंग्रेजी वर्णमाला का अक्षर 'D' किस प्रकार की परावर्तन समरूपता (अर्थात, दर्पण परावर्तन से संबंधित समरूपता) रखता है?
एक संख्या जब 143 से विभाजित की जाती है, तो यह 31 को शेषफल के रूप में छोड़ती है। जब उसी संख्या को 13 से विभाजित किया जाएगा, तो शेषफल क्या होगा?
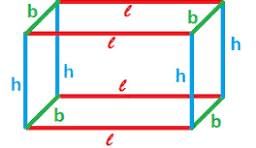
यदि घन की भुजा की लंबाई 4 सेमी है, तो इसका आयतन क्या होगा?
एक _____ संख्याओं का संग्रह है जिसे कुछ जानकारी देने के लिए इकट्ठा किया गया है।
अंग्रेजी वर्णमाला का अक्षर 'B' किस प्रकार की प्रतिबिंबीय समरूपता (यानी, दर्पण प्रतिबिंब से संबंधित समरूपता) रखता है?