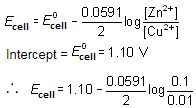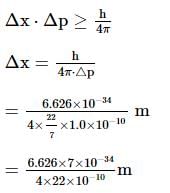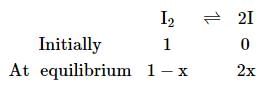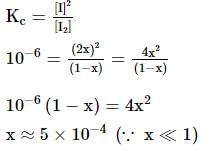VITEEE PCME Mock Test - 9 - JEE MCQ
30 Questions MCQ Test VITEEE: Subject Wise and Full Length MOCK Tests - VITEEE PCME Mock Test - 9
A second degree polynomial f(x) satisfies f(0) = 0, f(1) = 1, f′(x) > 0 for all x ∈ (0, 1). Then f(x) is
A linear programming problem of linear functions deals with
If ω is a complex cube root of unity, then the value of 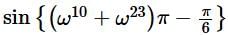 is
is
The equation of line through the point (1, 2) whose distance from the point (3, 1) has the greatest value, is
The value of λ and μ if (2î + 6ĵ + 27k̂) × (î + λĵ + μk̂) = 0 is:
If x/a + y/b = 2 touches the curve xⁿ/aⁿ + yⁿ/bⁿ = 2 at the point (α, β) and n, a, b ≠ 0, then:
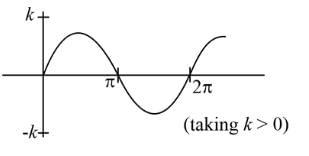
Area bounded by the curve y = k sin x and the x-axis between x = π and x = 2π is:
If α, β are the roots of the equation (x − a)(x − b) + c = 0, then the roots of the equation (x − α)(x − β) − c = 0 are:
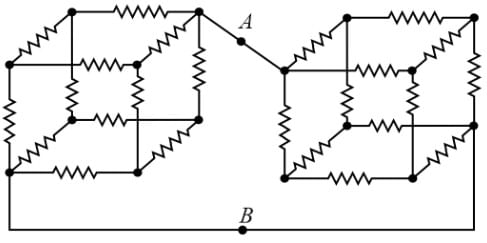
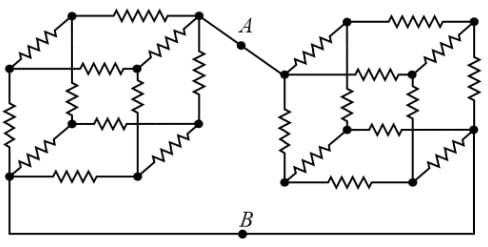
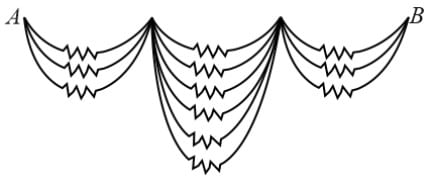
Consider the network of equal resistances (each R) shown in figure. Then the effective resistance between points A and B is
If the value of R is changed for the circuit given below, then

In the above figure, if the GeGe in the circled position is replaced by the GaGa, then the resultant forms which type of semiconductor?
The nucleus of atomic mass A and atomic number Z emits a β-particle. The atomic mass and atomic number of the resulting nucleus are
"When a Zener diode operates in the breakdown region, a current of 20 mA flows through it under an applied voltage of 80 V. What is the Zener impedance?"
If we throw a body upwards with a velocity of 4 m/s, then at what height does its kinetic energy reduce to half of the initial value? (Take g = 10 ms–2)
In a mass spectrometer used for measuring the masses of ions, the ions are initially accelerated by an electric potential V and then made to describe semicircular paths of radius R using a magnetic field B. If V and B are kept constant, the ratio 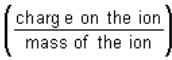 will be proportional to
will be proportional to
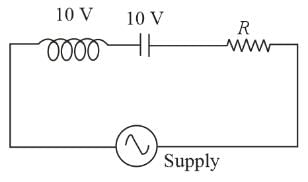
Ac source of voltage of V = V0sin (100t) is connected with box which contain either RL or RC circuit. If voltage leads the current by phase π/4, then:
The EMF of Daniell cell was found using different concentrations of Zn2+ ion and Cu2+ ion. A graph was then plotted between Ecell and The plot was found to be linear with intercept on Ecell axis equal to 1.10 V. Ecell for Zn/Zn2+ (0.1 M)
(Cu2+(0.01M) I Cu will be
The correct order of acidic strengths of the carboxylic acids is
If Aufbau principle is not followed, the atomic number of first f-block element will be:
The uncertainty in the momentum of an electron is 1.0 × 10⁻¹⁰ kg ms⁻¹. The uncertainty in its position will be; (h = 6.62 × 10⁻³⁴ Js)
If 1.0 mole of I₂ is introduced in a 1.0-liter flask at 1000 K (Kc = 10⁻⁶), which of the following statements is correct?
Choose the correct option to replace the word(s) given in brackets:
He seemed (have) finished his homework.
Study the table carefully to answer the questions that follow.
Profit (in ₹1000) made by six different shopkeepers over the months
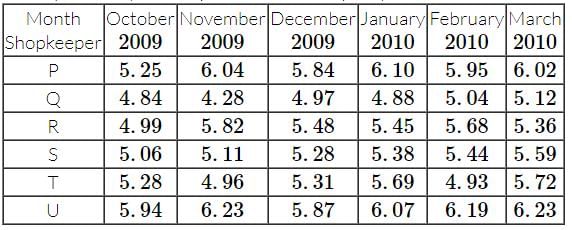
What is the difference in profit earned by shopkeeper T in January 2010 from the previous month?
|
1 videos|7 docs|63 tests
|
|
1 videos|7 docs|63 tests
|




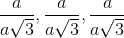 i.e.
i.e. 
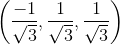
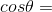
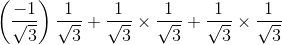 =
= 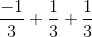 =
= 

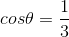
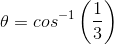

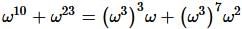
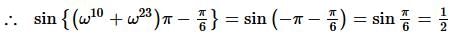
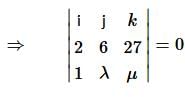

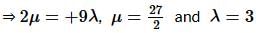
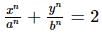
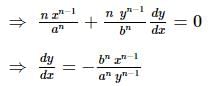
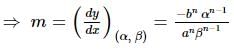
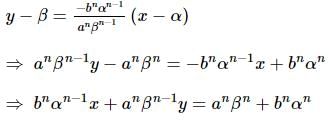
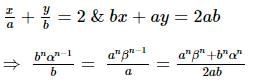
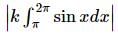
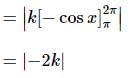

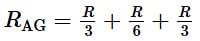
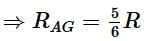
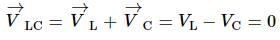




 is the centripetal force on the ion moving in a curved path of radius R.
is the centripetal force on the ion moving in a curved path of radius R.



 …(i)
…(i) or
or 

 (voltage lead, so Circuit is RL)
(voltage lead, so Circuit is RL)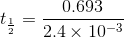 = 288.75 s
= 288.75 s 578 s
578 s