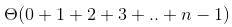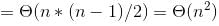Test: Asymptotic Worst Case Time & Space Complexity- 1 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Asymptotic Worst Case Time & Space Complexity- 1
What is recurrence for worst case of QuickSort and what is the time complexity in Worst case?
Suppose we have a O(n) time algorithm that finds median of an unsorted array. Now consider a QuickSort implementation where we first find median using the above algorithm, then use median as pivot. What will be the worst case time complexity of this modified QuickSort.
Given an unsorted array. The array has this property that every element in array is at most k distance from its position in sorted array where k is a positive integer smaller than size of array. Which sorting algorithm can be easily modified for sorting this array and what is the obtainable time complexity?
Which of the following is not true about comparison based sorting algorithms?
What is time complexity of fun()?
What is the time complexity of fun()?
The recurrence relation capturing the optimal time of the Tower of Hanoi problem with n discs is.
Let w(n) and A(n) denote respectively, the worst case and average case running time of an algorithm executed on an input of size n. which of the following is ALWAYS TRUE?
Which of the following is not O(n^2)?
Which of the given options provides the increasing order of asymptotic complexity of functions f1, f2, f3 and f4?
f1(n) = 2^n
f2(n) = n^(3/2)
f3(n) = nLogn
f4(n) = n^(Logn)
Consider the following program fragment for reversing the digits in a given integer to obtain a new integer. Let n = D1D2…Dm
Q. The loop invariant condition at the end of the ith iteration is:
What is the best time complexity of bubble sort?
What is the worst case time complexity of insertion sort where position of the data to be inserted is calculated using binary search?
The tightest lower bound on the number of comparisons, in the worst case, for comparison-based sorting is of the order of
In a modified merge sort, the input array is splitted at a position one-third of the length(N) of the array. What is the worst case time complexity of this merge sort?
What is the time complexity of the below function?
In a competition, four different functions are observed. All the functions use a single for loop and within the for loop, same set of statements are executed. Consider the following for loops:
Q. If n is the size of input(positive), which function is most efficient(if the task to be performed is not an issue)?
The following statement is valid. log(n!) = θ(n log n).
What does it mean when we say that an algorithm X is asymptotically more efficient than Y?
What is the time complexity of Floyd–Warshall algorithm to calculate all pair shortest path in a graph with n vertices?
|
55 docs|215 tests
|
|
55 docs|215 tests
|