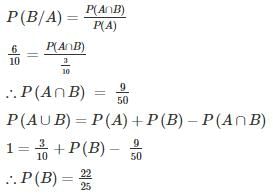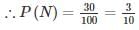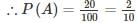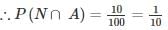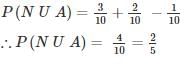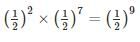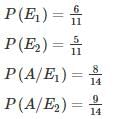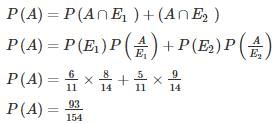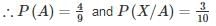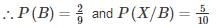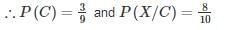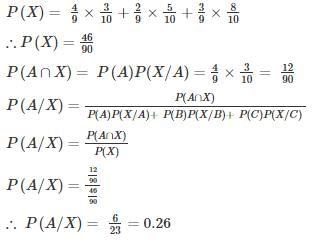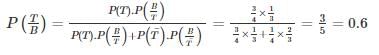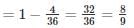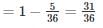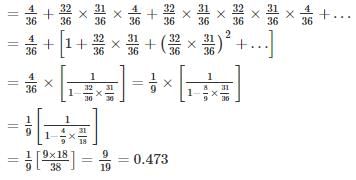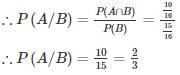Test: Engineering Mathematics- 7 - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Engineering Mathematics- 7
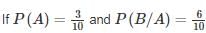 where A and B are exhaustive events, then find P(B)?
where A and B are exhaustive events, then find P(B)?
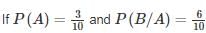 where A and B are exhaustive events, then find P(B)?
where A and B are exhaustive events, then find P(B)?In an examination, 20% of the students have failed in Computer Networks, 30% of the students have failed in Computer Architecture and 10% in Computer Networks and Computer Architecture. If a student is selected at random, then what is the probability that the student has failed in at least one subject?
A coin is tossed 9 times. What is the probability that the outcome of only first two tosses is headed?
A pair of dice is thrown. Find the probability of obtaining a sum of 8 or getting an even number on both the dice.
A bag contains 6 red, 5 blue balls, and another bag contains 5 red and 8 blue balls. A ball is drawn from the first bag without noticing the color is put in the second bag. A ball is drawn from the second bag. Find the probability that ball drawn is blue in color.
The chances of A, B, C becoming managers of a Testbook company are 4:2:3. The probability that the bonus scheme will be introduced if A, B, C become manager are 0.3, 0.5, 0.8 respectively.
If the bonus scheme has introduced, what is the probability that A is appointed as the manager of Testbook (answer up to 2 decimal place)?
A speaks truth 3 out of 4 times. There is a chance that match can be won, drawn or lost but A reported that Shyam has won the match. Find the probability that his report was correct.
A and B throw a pair of dice alternately. A wins if he throws faces with sum 5 before B throws faces with the sum of 6 and B wins if he throws faces with the sum of 6 before A throw faces with the sum of 5. If A begins, the chances of winning for A is________.
An anti-aircraft gun can take a maximum of 4 shots at an enemy plane moving away from it. The probabilities of hitting the plane at the first, second, third and fourth shot are 0.4, 0.3, 0.2 and 0.1 respectively. The probability that the gun hits the plane is_____
What is the probability of getting more than one tail given that at least one coin is head when 4 coins are tossed?
|
55 docs|215 tests
|
|
55 docs|215 tests
|