Test: Graphs- 2 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Graphs- 2
Which of the following algorithms can be used to most efficiently determine the presence of a cycle in a given graph ?
What are the appropriate data structures for following algorithms?
1) Breadth First Search
2) Depth First Search
3) Prim's Minimum Spanning Tree
4) Kruskal' Minimum Spanning Tree
2) Depth First Search
3) Prim's Minimum Spanning Tree
4) Kruskal' Minimum Spanning Tree
The Breadth First Search algorithm has been implemented using the queue data structure. One possible order of visiting the nodes of the following graph is
Let G be an undirected graph. Consider a depth-first traversal of G, and let T be the resulting depth-first search tree. Let u be a vertex in G and let v be the first new (unvisited) vertex visited after visiting u in the traversal. Which of the following statements is always true? (GATE CS 2000)
Consider the following graph
Among the following sequences
I) a b e g h f
II) a b f e h g
III) a b f h g e
IV) a f g h b e
Q. Which are depth first traversals of the above graph?
Make is a utility that automatically builds executable programs and libraries from source code by reading files called makefiles which specify how to derive the target program. Which of the following standard graph algorithms is used by Make.
Given two vertices in a graph s and t, which of the two traversals (BFS and DFS) can be used to find if there is path from s to t?
Which of the following condition is sufficient to detect cycle in a directed graph?
Is following statement true/false If a DFS of a directed graph contains a back edge, any other DFS of the same graph will also contain at least one back edge
Is following statement true/false? A DFS of a directed graph always produces the same number of tree edges, i.e., independent of the order in which vertices are considered for DFS.
If the DFS finishing time f[u] > f[v] for two vertices u and v in a directed graph G, and u and v are in the same DFS tree in the DFS forest, then u is an ancestor of v in the depth first tree.
Consider the DAG with Consider V = {1, 2, 3, 4, 5, 6}, shown below. Which of the following is NOT a topological ordering?
Let G be a graph with n vertices and m edges. What is the tightest upper bound on the running time on Depth First Search of G? Assume that the graph is represented using adjacency matrix.
Consider the tree arcs of a BFS traversal from a source node W in an unweighted, connected, undirected graph. The tree T formed by the tree arcs is a data structure for computing.
Suppose depth first search is executed on the graph below starting at some unknown vertex. Assume that a recursive call to visit a vertex is made only after first checking that the vertex has not been visited earlier. Then the maximum possible recursion depth (including the initial call) is
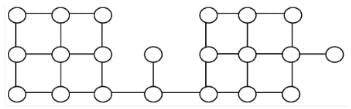
Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?
Let G be an undirected graph. Consider a depth-first traversal of G, and let T be the resulting depth-first search tree. Let u be a vertex in G and let v be the first new (unvisited) vertex visited after visiting u in the traversal. Which of the following statements is always true?
In a depth-first traversal of a graph G with n vertices, k edges are marked as tree edges. The number of connected components in G is
Consider the following directed graph.
Q. The number of different topological orderings of the vertices of the graph is
Note : This question was asked as Numerical Answer Type.
|
55 docs|215 tests
|
|
55 docs|215 tests
|




















